Solutions de défi du générateur de séries de nombres - Partie 4

Ceci est la quatrième partie d'une série sur les solutions au défi du générateur de séries de nombres. Un grand merci à Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea et Paul White pour avoir partagé vos idées et commentaires.

J'adore le travail de Paul White. Je continue d'être choqué par ses découvertes et je me demande comment diable il comprend ce qu'il fait. J'aime aussi son style d'écriture efficace et éloquent. Souvent, en lisant ses articles ou ses messages, je secoue la tête et dis à ma femme, Lilach, que quand je serai grand, je veux être comme Paul.

Lorsque j'ai initialement publié le défi, j'espérais secrètement que Paul publierait une solution. Je savais que s'il le faisait, ce serait très spécial. Eh bien, il l'a fait, et c'est fascinant! Il a d'excellentes performances et vous pouvez en apprendre beaucoup. Cet article est dédié à la solution de Paul.

Je vais faire mes tests dans tempdb, en activant les statistiques d'E/S et de temps :

SET NOCOUNT ON;
 
USE tempdb;
 
SET STATISTICS TIME, IO ON;

Limites des idées précédentes

En évaluant les solutions antérieures, l'un des facteurs importants pour obtenir de bonnes performances était la possibilité d'utiliser le traitement par lots. Mais l'avons-nous exploité au maximum ?

Examinons les plans de deux des solutions précédentes qui utilisaient le traitement par lots. Dans la partie 1, j'ai couvert la fonction dbo.GetNumsAlanCharlieItzikBatch, qui combinait les idées d'Alan, de Charlie et de moi-même.

Voici la définition de la fonction :

-- Helper dummy table
DROP TABLE IF EXISTS dbo.BatchMe;
GO
 
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO
 
-- Function definition
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  WITH
    L0 AS ( SELECT 1 AS c
            FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
                        (1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
    L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
    L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
    L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
    Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
              FROM L3 )
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
 
     @low - 1 + rownum AS n
  FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
  ORDER BY rownum;
GO

Cette solution définit un constructeur de valeur de table de base avec 16 lignes et une série de CTE en cascade avec des jointures croisées pour gonfler le nombre de lignes à potentiellement 4B. La solution utilise la fonction ROW_NUMBER pour créer la séquence de base de nombres dans un CTE appelé Nums, et le filtre TOP pour filtrer la cardinalité de la série de nombres souhaitée. Pour activer le traitement par lots, la solution utilise une jointure gauche factice avec une condition fausse entre le CTE Nums et une table appelée dbo.BatchMe, qui a un index columnstore.

Utilisez le code suivant pour tester la fonction avec la technique d'affectation de variables :

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

La représentation de Plan Explorer de la réelle le plan de cette exécution est illustré à la figure 1.

Figure 1 :Plan pour la fonction dbo.GetNumsAlanCharlieItzikBatch

Lors de l'analyse du mode batch par rapport au traitement en mode ligne, il est assez agréable de pouvoir dire simplement en regardant un plan à un niveau élevé quel mode de traitement chaque opérateur a utilisé. En effet, Plan Explorer affiche un chiffre de lot bleu clair dans la partie inférieure gauche de l'opérateur lorsque son mode d'exécution réel est Lot. Comme vous pouvez le voir sur la figure 1, le seul opérateur qui utilise le mode batch est l'opérateur Window Aggregate, qui calcule les numéros de ligne. Il y a encore beaucoup de travail effectué par d'autres opérateurs en mode ligne.

Voici les chiffres de performance que j'ai obtenus lors de mon test :

logique lit 0

Pour identifier les opérateurs qui ont mis le plus de temps à s'exécuter, utilisez l'option Plan d'exécution réel dans SSMS ou l'option Obtenir le plan réel dans Plan Explorer. Assurez-vous de lire l'article récent de Paul Comprendre les horaires des opérateurs du plan d'exécution. L'article décrit comment normaliser les temps d'exécution des opérateurs signalés afin d'obtenir les chiffres corrects.

Dans le plan de la figure 1, la majeure partie du temps est consacrée aux opérateurs Nested Loops et Top les plus à gauche, tous deux exécutés en mode ligne. Outre le fait que le mode ligne est moins efficace que le mode batch pour les opérations intensives du processeur, gardez également à l'esprit que le passage du mode ligne au mode batch et inversement prend un péage supplémentaire.

Dans la partie 2, j'ai couvert une autre solution utilisant le traitement par lots, implémentée dans la fonction dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2. Cette solution combinait les idées de John Number2, Dave Mason, Joe Obbish, Alan, Charlie et moi-même. La principale différence entre la solution précédente et celle-ci est qu'en tant qu'unité de base, la première utilise un constructeur de valeur de table virtuelle et la seconde utilise une table réelle avec un index columnstore, vous offrant un traitement par lots "gratuitement". Voici le code qui crée la table et la remplit à l'aide d'une instruction INSERT avec 102 400 lignes pour la compresser :

DROP TABLE IF EXISTS dbo.NullBits102400;
GO
 
CREATE TABLE dbo.NullBits102400
(
  b BIT NULL, 
  INDEX cc_NullBits102400 CLUSTERED COLUMNSTORE
    WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
 
WITH
  L0 AS (SELECT CAST(NULL AS BIT) AS b
         FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
  L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
  nulls(b) AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B CROSS JOIN L1 AS C)
INSERT INTO dbo.NullBits102400 WITH (TABLOCK) (b) 
  SELECT TOP(102400) b FROM nulls;
GO

Voici la définition de la fonction :

CREATE OR ALTER FUNCTION dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2
  (@low AS BIGINT = 1, @high AS BIGINT) RETURNS TABLE
AS
RETURN
  WITH
    Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
             FROM dbo.NullBits102400 AS A
               CROSS JOIN dbo.NullBits102400 AS B)
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
     @low - 1 + rownum AS n
  FROM Nums
  ORDER BY rownum;
GO

Une seule jointure croisée entre deux instances de la table de base est suffisante pour produire bien au-delà du potentiel souhaité de 4B lignes. Ici encore, la solution utilise la fonction ROW_NUMBER pour produire la séquence de base des nombres et le filtre TOP pour restreindre la cardinalité de la série de nombres souhaitée.

Voici le code pour tester la fonction en utilisant la technique d'affectation de variables :

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);

Le plan de cette exécution est illustré à la figure 2.

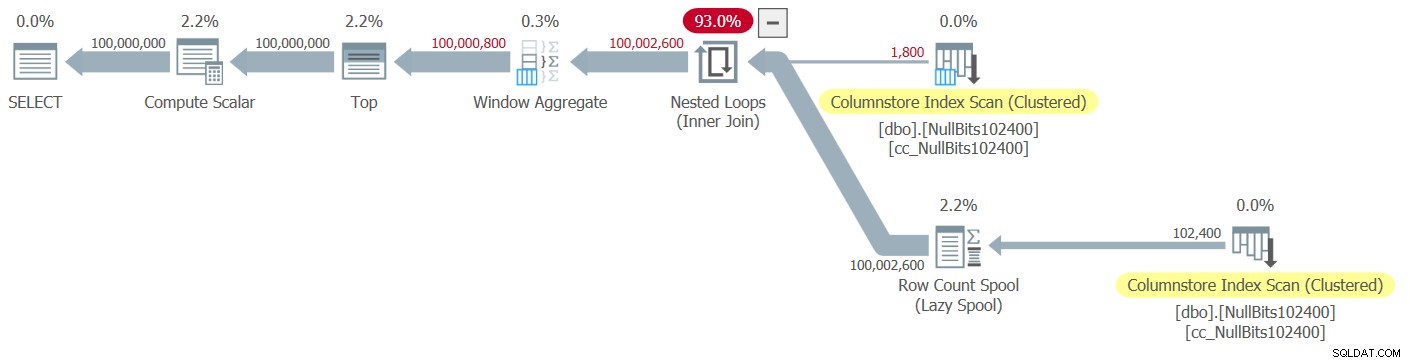Figure 2 :Plan pour la fonction dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2

Observez que seuls deux opérateurs de ce plan utilisent le mode batch :le balayage supérieur de l'index clustered columnstore de la table, qui est utilisé comme entrée externe de la jointure Nested Loops, et l'opérateur Window Aggregate, qui est utilisé pour calculer les numéros de lignes de base. .

J'ai obtenu les chiffres de performance suivants pour mon test :

Tableau 'NullBits102400'. Nombre de balayages 2, lectures logiques 0, lectures physiques 0, lectures du serveur de pages 0, lectures anticipées 0, lectures anticipées du serveur de pages 0, lectures logiques lob 8, lectures physiques lob 0, lectures du serveur de pages lob 0, lectures lob- l'avance lit 0, la lecture anticipée du serveur de pages lob lit 0.

Tableau 'NullBits102400'. Segment lit 2, segment ignoré 0.

Encore une fois, la plupart du temps dans l'exécution de ce plan est passé par les boucles imbriquées et les opérateurs supérieurs les plus à gauche, qui s'exécutent en mode ligne.

La solution de Paul

Avant de présenter la solution de Paul, je vais commencer par ma théorie concernant le processus de pensée qu'il a traversé. C'est en fait un excellent exercice d'apprentissage, et je vous suggère de le parcourir avant de regarder la solution. Paul a reconnu les effets débilitants d'un plan qui mélange à la fois les modes par lots et par lignes, et s'est lancé le défi de trouver une solution qui obtienne un plan tout en mode par lots. En cas de succès, le potentiel pour une telle solution de bien fonctionner est assez élevé. Il est certainement fascinant de voir si un tel objectif est même réalisable étant donné qu'il existe encore de nombreux opérateurs qui ne prennent pas encore en charge le mode par lots et de nombreux facteurs qui inhibent le traitement par lots. Par exemple, au moment de la rédaction, le seul algorithme de jointure qui prend en charge le traitement par lots est l'algorithme de jointure par hachage. Une jointure croisée est optimisée à l'aide de l'algorithme de boucles imbriquées. De plus, l'opérateur Top n'est actuellement implémenté qu'en mode ligne. Ces deux éléments sont des éléments fondamentaux essentiels utilisés dans les plans de bon nombre des solutions que j'ai abordées jusqu'à présent, y compris les deux ci-dessus.

En supposant que vous ayez relevé le défi de créer une solution avec un plan entièrement en mode batch, passons au deuxième exercice. Je vais d'abord présenter la solution de Paul telle qu'il l'a fournie, avec ses commentaires en ligne. Je vais également le lancer pour comparer ses performances avec les autres solutions. J'ai beaucoup appris en déconstruisant et en reconstruisant sa solution, une étape à la fois, pour m'assurer de bien comprendre pourquoi il a utilisé chacune des techniques qu'il a utilisées. Je vous suggère de faire de même avant de passer à la lecture de mes explications.

Voici la solution de Paul, qui implique une table de stockage de colonnes d'assistance appelée dbo.CS et une fonction appelée dbo.GetNums_SQLkiwi :

-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
 
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
    -- type as integer NOT NULL
    -- (everything is normalized to 64 bits in columnstore/batch mode anyway)
    n1 = ISNULL(CONVERT(integer, 0), 0), 
    n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM 
(
    SELECT
        rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
    FROM master.dbo.spt_values AS SV1
    CROSS JOIN master.dbo.spt_values AS SV2
    ORDER BY 
        rn ASC
        OFFSET 0 ROWS
        FETCH NEXT 65536 ROWS ONLY
) AS N;
 
-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS 
WITH (MAXDOP = 1);
GO
 
-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scala
        @low - 2 + N.rn < @high;
GO

Voici le code que j'ai utilisé pour tester la fonction avec la technique d'affectation de variables :

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000);

J'ai obtenu le plan illustré à la figure 3 pour mon test.

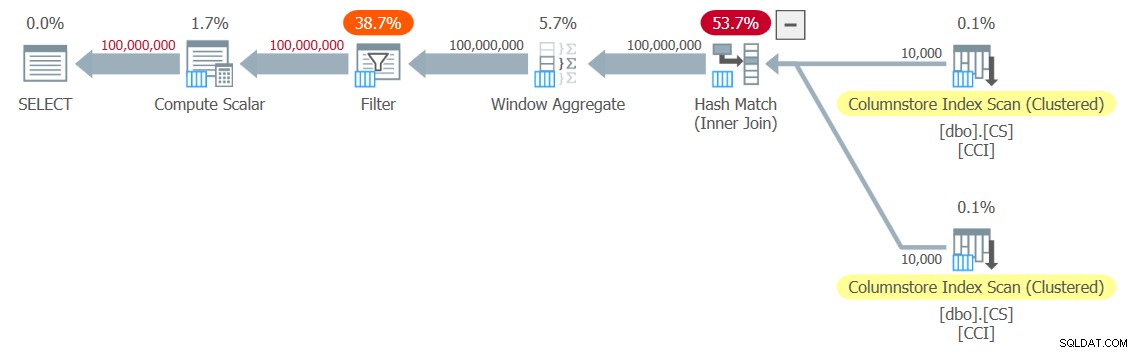Figure 3 :Plan pour la fonction dbo.GetNums_SQLkiwi

C'est un plan tout en mode batch! C'est assez impressionnant.

Voici les chiffres de performance que j'ai obtenus pour ce test sur ma machine :

Tableau 'SC'. Nombre de balayages 2, lectures logiques 0, lectures physiques 0, lectures du serveur de pages 0, lectures anticipées 0, lectures anticipées du serveur de pages 0, lectures logiques lob 44, lectures physiques lob 0, lectures du serveur de pages lob 0, lectures lob- l'avance lit 0, la lecture anticipée du serveur de pages lob lit 0.

Tableau 'SC'. Segment lit 2, segment ignoré 0.

Vérifions également que si vous devez renvoyer les nombres ordonnés par n, la solution préserve l'ordre par rapport à rn - du moins lorsque vous utilisez des constantes comme entrées - et évitez ainsi un tri explicite dans le plan. Voici le code pour le tester avec la commande :

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n;

Vous obtenez le même plan que dans la figure 3, et donc des performances similaires :

Tableau 'CS'. Nombre de balayages 2, lectures logiques 0, lectures physiques 0, lectures du serveur de pages 0, lectures anticipées 0, lectures anticipées du serveur de pages 0, lectures logiques lob 44, lectures physiques lob 0, lectures du serveur de pages lob 0, lectures lob- l'avance lit 0, la lecture anticipée du serveur de pages lob lit 0.

Tableau 'CS'. Segment lit 2, segment ignoré 0.

C'est un aspect important de la solution.

Modification de notre méthodologie de test

Les performances de la solution de Paul sont une amélioration décente du temps écoulé et du temps CPU par rapport aux deux solutions précédentes, mais cela ne semble pas être l'amélioration la plus spectaculaire que l'on pourrait attendre d'un plan en mode tout-batch. Peut-être qu'il nous manque quelque chose ?

Essayons d'analyser les temps d'exécution de l'opérateur en examinant le plan d'exécution réel dans SSMS, comme illustré à la figure 4.

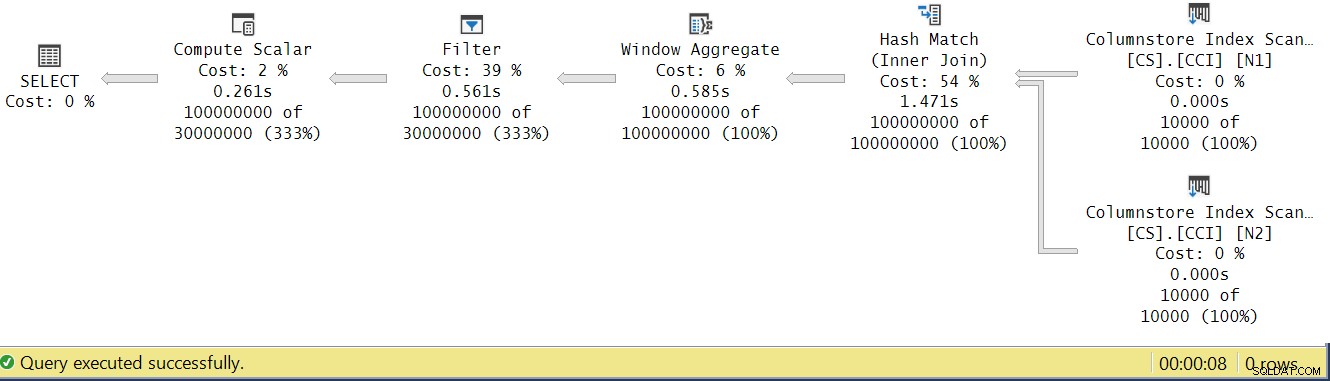Figure 4 :temps d'exécution de l'opérateur pour la fonction dbo.GetNums_SQLkiwi

Dans l'article de Paul sur l'analyse des temps d'exécution des opérateurs, il explique qu'avec les opérateurs en mode batch, chacun rapporte son propre temps d'exécution. Si vous additionnez les temps d'exécution de tous les opérateurs de ce plan réel, vous obtiendrez 2,878 secondes, mais le plan a mis 7,876 secondes à s'exécuter. 5 secondes du temps d'exécution semblent manquer. La réponse à cela réside dans la technique de test que nous utilisons, avec l'affectation de variables. Rappelez-vous que nous avons décidé d'utiliser cette technique pour éliminer le besoin d'envoyer toutes les lignes du serveur à l'appelant et pour éviter les E/S qui seraient impliquées dans l'écriture du résultat dans une table. Cela semblait être l'option parfaite. Cependant, le véritable coût de l'affectation des variables est masqué dans ce plan et, bien entendu, il s'exécute en mode ligne. Mystère résolu.

Évidemment, en fin de compte, un bon test est un test qui reflète adéquatement votre utilisation de la solution en production. Si vous écrivez généralement les données dans une table, vous avez besoin que votre test reflète cela. Si vous envoyez le résultat à l'appelant, vous avez besoin que votre test reflète cela. Quoi qu'il en soit, l'affectation de variables semble représenter une grande partie du temps d'exécution dans notre test, et il est clair qu'il est peu probable qu'elle représente une utilisation typique de la fonction en production. Paul a suggéré qu'au lieu d'assigner des variables, le test pourrait appliquer un simple agrégat comme MAX à la colonne de nombre renvoyée (n/rn/op). Un opérateur d'agrégation peut utiliser le traitement par lots, de sorte que le plan n'impliquerait pas de conversion du mode par lots au mode ligne à la suite de son utilisation, et sa contribution au temps d'exécution total devrait être assez faible et connue.

Retestons donc les trois solutions abordées dans cet article. Voici le code pour tester la fonction dbo.GetNumsAlanCharlieItzikBatch :

SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

J'ai obtenu le plan illustré à la figure 5 pour ce test.

Figure 5 :Plan pour la fonction dbo.GetNumsAlanCharlieItzikBatch avec agrégat

Voici les chiffres de performance que j'ai obtenus pour ce test :

logique lit 0

Observez que le temps d'exécution est passé de 10,025 secondes en utilisant la technique d'affectation de variables à 8,733 en utilisant la technique d'agrégation. C'est un peu plus d'une seconde de temps d'exécution que nous pouvons attribuer à l'affectation de variable ici.

Voici le code pour tester la fonction dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2 :

SELECT MAX(n) AS mx FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);

J'ai obtenu le plan illustré à la figure 6 pour ce test.

Figure 6 :Plan pour la fonction dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2 avec agrégat

Voici les chiffres de performance que j'ai obtenus pour ce test :

Tableau 'NullBits102400'. Nombre de balayages 2, lectures logiques 0, lectures physiques 0, lectures du serveur de pages 0, lectures anticipées 0, lectures anticipées du serveur de pages 0, lectures logiques lob 8, lectures physiques lob 0, lectures du serveur de pages lob 0, lectures lob- l'avance lit 0, la lecture anticipée du serveur de pages lob lit 0.

Tableau 'NullBits102400'. Segment lit 2, segment ignoré 0.

Observez que le temps d'exécution est passé de 9,813 secondes en utilisant la technique d'affectation de variables à 7,053 en utilisant la technique d'agrégation. C'est un peu plus de deux secondes de temps d'exécution que nous pouvons attribuer à l'affectation de variable ici.

Et voici le code pour tester la solution de Paul :

SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);

J'obtiens le plan illustré à la figure 7 pour ce test.

Figure 7 :Plan pour la fonction dbo.GetNums_SQLkiwi avec agrégat

Et maintenant pour le grand moment. J'ai obtenu les chiffres de performance suivants pour ce test :

Tableau 'SC'. Nombre de balayages 2, lectures logiques 0, lectures physiques 0, lectures du serveur de pages 0, lectures anticipées 0, lectures anticipées du serveur de pages 0, lectures logiques lob 44, lectures physiques lob 0, lectures du serveur de pages lob 0, lectures lob- l'avance lit 0, la lecture anticipée du serveur de pages lob lit 0.

Tableau 'SC'. Segment lit 2, segment ignoré 0.

Le temps d'exécution est passé de 7,822 secondes à 3,149 secondes ! Examinons les temps d'exécution de l'opérateur dans le plan réel dans SSMS, comme illustré à la figure 8.

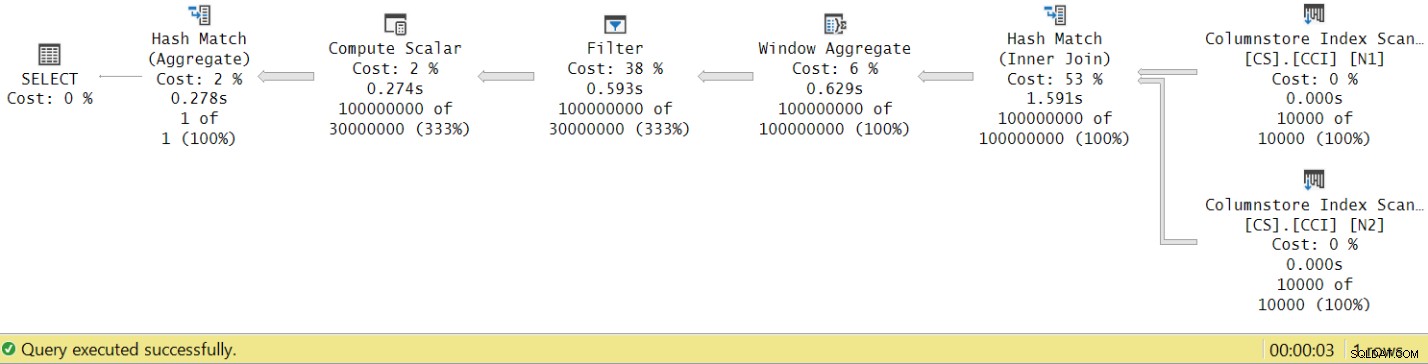Figure 8 :temps d'exécution de l'opérateur pour la fonction dbo.GetNums avec agrégat

Maintenant, si vous accumulez les temps d'exécution des opérateurs individuels, vous obtiendrez un nombre similaire au temps d'exécution total du plan.

La figure 9 présente une comparaison des performances en termes de temps écoulé entre les trois solutions en utilisant à la fois les techniques d'affectation de variables et de test agrégé.

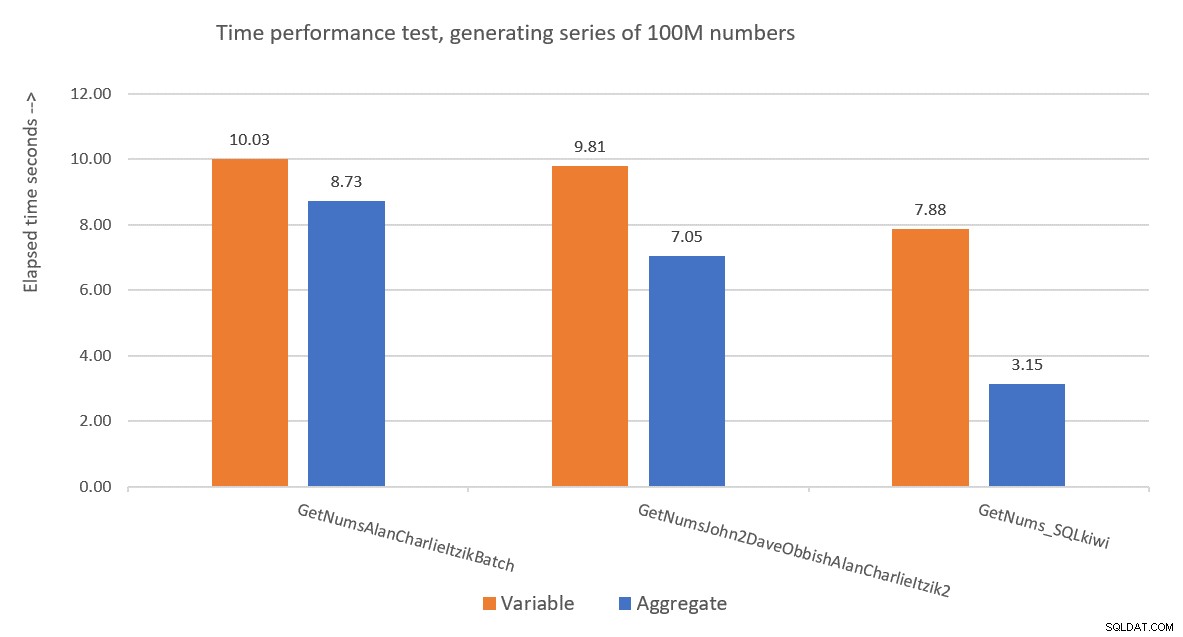Figure 9 :Comparaison des performances

La solution de Paul est clairement gagnante, et cela est particulièrement évident lors de l'utilisation de la technique de test agrégé. Quel exploit impressionnant !

Déconstruire et reconstruire la solution de Paul

Déconstruire puis reconstruire la solution de Paul est un excellent exercice, et vous apprendrez beaucoup en le faisant. Comme suggéré précédemment, je vous recommande de suivre le processus vous-même avant de continuer à lire.

Le premier choix que vous devez faire est la technique que vous utiliseriez pour générer le nombre potentiel souhaité de rangées de 4B. Paul a choisi d'utiliser une table columnstore et de la remplir avec autant de lignes que la racine carrée du nombre requis, soit 65 536 lignes, de sorte qu'avec une seule jointure croisée, vous obteniez le nombre requis. Vous pensez peut-être qu'avec moins de 102 400 lignes, vous n'obtiendrez pas un groupe de lignes compressé, mais cela s'applique lorsque vous remplissez la table avec une instruction INSERT comme nous l'avons fait avec la table dbo.NullBits102400. Cela ne s'applique pas lorsque vous créez un index columnstore sur une table préremplie. Paul a donc utilisé une instruction SELECT INTO pour créer et remplir la table sous la forme d'un tas basé sur un magasin de lignes avec 65 536 lignes, puis a créé un index de magasin de colonnes en cluster, ce qui a donné un groupe de lignes compressé.

Le prochain défi consiste à déterminer comment faire en sorte qu'une jointure croisée soit traitée avec un opérateur en mode batch. Pour cela, vous avez besoin que l'algorithme de jointure soit un hachage. N'oubliez pas qu'une jointure croisée est optimisée à l'aide de l'algorithme de boucles imbriquées. Vous devez d'une manière ou d'une autre tromper l'optimiseur pour qu'il pense que vous utilisez une équijointure interne (le hachage nécessite au moins un prédicat basé sur l'égalité), mais obtenez une jointure croisée dans la pratique.

Une première tentative évidente consiste à utiliser une jointure interne avec un prédicat de jointure artificielle qui est toujours vrai, comme ceci :

SELECT *
FROM dbo.CS AS N1
  INNER HASH JOIN dbo.CS AS N2
    ON 0 = 0;

Mais ce code échoue avec l'erreur suivante :

L'optimiseur de SQL Server reconnaît qu'il s'agit d'un prédicat artificiel de jointure interne, simplifie la jointure interne en une jointure croisée et génère une erreur indiquant qu'il ne peut pas accepter l'indication pour forcer un algorithme de jointure par hachage.

Pour résoudre ce problème, Paul a créé une colonne INT NOT NULL (plus d'informations sur la raison de cette spécification sous peu) appelée n1 dans sa table dbo.CS et l'a remplie avec 0 dans toutes les lignes. Il a ensuite utilisé le prédicat de jointure N2.n1 =N1.n1, obtenant effectivement la proposition 0 =0 dans toutes les évaluations de correspondance, tout en respectant les exigences minimales d'un algorithme de jointure par hachage.

Cela fonctionne et produit un plan tout en mode batch :

SELECT *
FROM dbo.CS AS N1
  INNER HASH JOIN dbo.CS AS N2
    ON N2.n1 = N1.n1;

Quant à la raison pour laquelle n1 doit être défini comme INT NOT NULL ; pourquoi interdire les NULL et pourquoi ne pas utiliser BIGINT ? La raison de ces choix est d'éviter un résidu de sonde de hachage (un filtre supplémentaire appliqué par l'opérateur de jointure par hachage au-delà du prédicat de jointure d'origine), ce qui pourrait entraîner des coûts supplémentaires inutiles. Voir l'article de Paul Join Performance, Implicit Conversions, and Residuals pour plus de détails. Voici la partie de l'article qui nous concerne :

Notez que cette optimisation ne s'applique pas aux colonnes bigint."

Pour vérifier cet aspect, créons une autre table appelée dbo.CS2 avec une colonne n1 nullable :

DROP TABLE IF EXISTS dbo.CS2;
 
SELECT * INTO dbo.CS2 FROM dbo.CS;
 
ALTER TABLE dbo.CS2 ALTER COLUMN n1 INT NULL;
 
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS2
WITH (MAXDOP = 1);

Testons d'abord une requête sur dbo.CS (où n1 est défini comme INT NOT NULL), en générant des numéros de ligne de base 4B dans une colonne appelée rn et en appliquant l'agrégat MAX à la colonne :

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS AS N1
    JOIN dbo.CS AS N2
        ON N2.n1 = N1.n1
) AS N;

Nous allons comparer le plan de cette requête avec le plan d'une requête similaire contre dbo.CS2 (où n1 est défini comme INT NULL) :

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS2 AS N1
    JOIN dbo.CS2 AS N2
        ON N2.n1 = N1.n1
) AS N;

Les plans pour les deux requêtes sont illustrés à la figure 10.

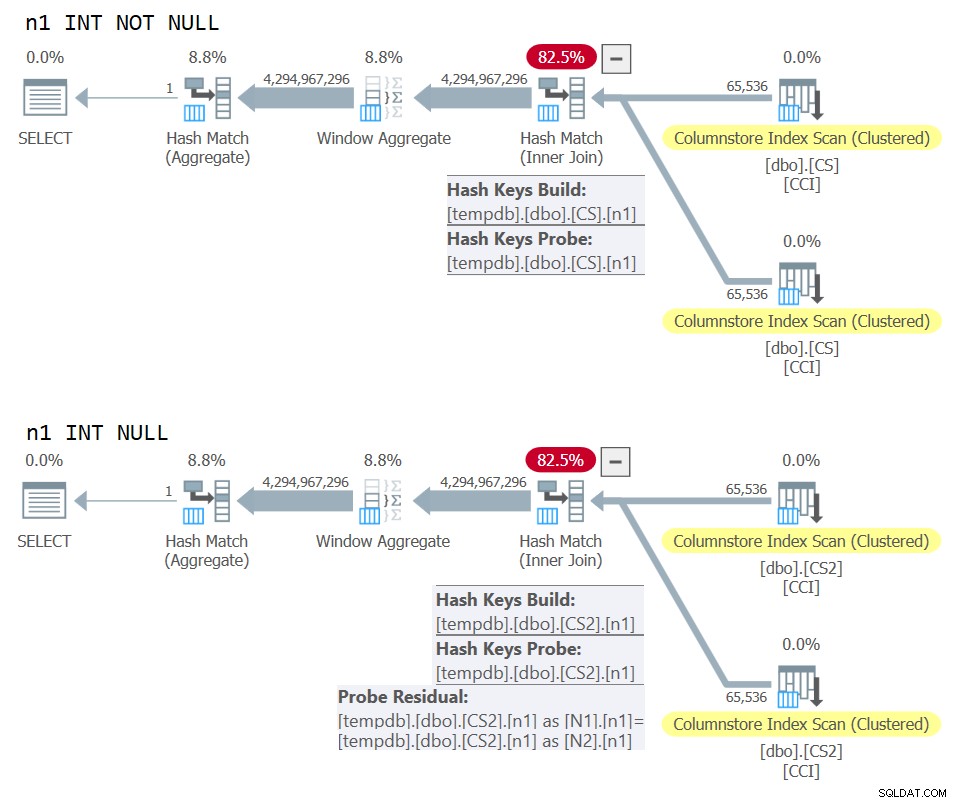Figure 10 :Plan de comparaison pour la clé de jointure NOT NULL vs NULL

Vous pouvez clairement voir le résidu de sonde supplémentaire qui est appliqué dans le deuxième plan mais pas dans le premier.

Sur ma machine, la requête contre dbo.CS s'est terminée en 91 secondes et la requête contre dbo.CS2 s'est terminée en 92 secondes. Dans l'article de Paul, il signale une différence de 11 % en faveur du cas NOT NULL pour l'exemple qu'il a utilisé.

BTW, ceux d'entre vous qui ont un œil attentif auront remarqué l'utilisation de ORDER BY @@TRANCOUNT comme spécification de commande de la fonction ROW_NUMBER. Si vous lisez attentivement les commentaires en ligne de Paul dans sa solution, il mentionne que l'utilisation de la fonction @@TRANCOUNT est un inhibiteur de parallélisme, alors que l'utilisation de @@SPID ne l'est pas. Vous pouvez donc utiliser @@TRANCOUNT comme constante d'exécution dans la spécification de commande lorsque vous souhaitez forcer un plan série et @@SPID dans le cas contraire.

Comme mentionné, il a fallu 91 secondes à la requête contre dbo.CS pour s'exécuter sur ma machine. À ce stade, il pourrait être intéressant de tester le même code avec une véritable jointure croisée, laissant l'optimiseur utiliser un algorithme de jointure de boucles imbriquées en mode ligne :

SELECT
    mx = MAX(N.rn)
FROM
(
    SELECT 
        rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
    FROM dbo.CS AS N1
    CROSS JOIN dbo.CS AS N2
) AS N;

Il a fallu 104 secondes pour terminer ce code sur ma machine. Nous obtenons donc une amélioration considérable des performances avec la jointure par hachage en mode batch.

Notre problème suivant est le fait que lorsque vous utilisez TOP pour filtrer le nombre de lignes souhaité, vous obtenez un plan avec un opérateur Top en mode ligne. Voici une tentative d'implémentation de la fonction dbo.GetNums_SQLkiwi avec un filtre TOP :

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT TOP (100000000 - 1 + 1)
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        ORDER BY rn
    ) AS N;
GO

Testons la fonction :

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

J'ai obtenu le plan illustré à la figure 11 pour ce test.

Figure 11 :Plan avec filtre TOP

Notez que l'opérateur Top est le seul du plan qui utilise le traitement en mode ligne.

J'ai obtenu les statistiques de temps suivantes pour cette exécution :

La plus grande partie du temps d'exécution de ce plan est consacrée à l'opérateur supérieur en mode ligne et au fait que le plan doit passer par une conversion par lot en mode ligne et vice-versa.

Notre défi est de trouver une alternative de filtrage en mode batch au TOP en mode ligne. Les filtres basés sur des prédicats comme ceux appliqués avec la clause WHERE peuvent potentiellement être gérés avec un traitement par lots.

L'approche de Paul consistait à introduire une deuxième colonne de type INT (voir le commentaire en ligne "tout est normalisé en 64 bits en mode columnstore/batch de toute façon" ) a appelé n2 dans la table dbo.CS et remplissez-la avec la séquence d'entiers comprise entre 1 et 65 536. Dans le code de la solution, il a utilisé deux filtres basés sur des prédicats. L'un est un filtre grossier dans la requête interne avec des prédicats impliquant la colonne n2 des deux côtés de la jointure. Ce filtre grossier peut entraîner des faux positifs. Voici la première tentative simpliste d'un tel filtre :

WHERE
    -- Coarse filter:
    N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))

Avec les entrées 1 et 100 000 000 comme @low et @high, vous n'obtenez aucun faux positif. Mais essayez avec 1 et 100 000 001, et vous en obtiendrez. Vous obtiendrez une séquence de 100 020 001 numéros au lieu de 100 000 001.

Pour éliminer les faux positifs, Paul a ajouté un deuxième filtre précis impliquant la colonne rn dans la requête externe. Voici la première tentative simpliste d'un filtre aussi précis :

WHERE
    -- Precise filter:
    N.rn < @high - @low + 2

Révisons la définition de la fonction pour utiliser les filtres basés sur les prédicats ci-dessus au lieu de TOP, prenez 1 :

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT
            rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        WHERE
            -- Coarse filter:
            N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    ) AS N
    WHERE
        -- Precise filter:
        N.rn < @high - @low + 2;
GO

Testons la fonction :

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

J'ai obtenu le plan illustré à la figure 12 pour ce test.

Figure 12 :Plan avec le filtre WHERE, prise 1

Hélas, quelque chose a clairement mal tourné. SQL Server a converti notre filtre basé sur les prédicats impliquant la colonne rn en un filtre basé sur TOP et l'a optimisé avec un opérateur Top, ce qui est exactement ce que nous avons essayé d'éviter. Pour ajouter l'insulte à l'injure, l'optimiseur a également décidé d'utiliser l'algorithme de boucles imbriquées pour la jointure.

Il a fallu 18,8 secondes à ce code pour terminer sur ma machine. Ça n'a pas l'air bien.

En ce qui concerne la jointure de boucles imbriquées, c'est quelque chose dont nous pourrions facilement nous occuper en utilisant un indice de jointure dans la requête interne. Juste pour voir l'impact sur les performances, voici un test avec un indicateur de requête de jointure par hachage forcé utilisé dans la requête de test elle-même :

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(HASH JOIN);

Le temps d'exécution est réduit à 13,2 secondes.

Nous avons toujours le problème avec la conversion du filtre WHERE contre rn en un filtre TOP. Essayons de comprendre comment cela s'est passé. Nous avons utilisé le filtre suivant dans la requête externe :

WHERE N.rn < @high - @low + 2

N'oubliez pas que rn représente une expression basée sur ROW_NUMBER non manipulée. Un filtre basé sur une telle expression non manipulée se trouvant dans une plage donnée est souvent optimisé avec un opérateur Top, ce qui pour nous est une mauvaise nouvelle en raison de l'utilisation du traitement en mode ligne.

La solution de contournement de Paul était d'utiliser un prédicat équivalent, mais qui applique la manipulation à rn, comme ceci :

WHERE @low - 2 + N.rn < @high

Le filtrage d'une expression qui ajoute une manipulation à une expression basée sur ROW_NUMBER inhibe la conversion du filtre basé sur le prédicat en un filtre basé sur TOP. C'est génial !

Révisons la définition de la fonction pour utiliser le prédicat WHERE ci-dessus, prenez 2 :

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT
            rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            ON N2.n1 = N1.n1
        WHERE
            -- Coarse filter:
            N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
    ) AS N
    WHERE
        -- Precise filter:
        @low - 2 + N.rn < @high;
GO

Test the function again, without any special hints or anything:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

It naturally gets an all-batch-mode plan with a hash join algorithm and no Top operator, resulting in an execution time of 3.177 seconds. Looking good.

The next step is to check if the solution handles bad inputs well. Let’s try it with a negative delta:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);

This execution fails with the following error.

Paul’s solution involved two additions. One is to add the following predicate to the inner query’s WHERE clause:

 @high >= @low

This filter does more than what it seems initially. If you’ve read Paul’s inline comments carefully, you could find this part:

The intriguing part here is the potential to use a constant scan with constants as inputs. I’ll get to this shortly.

The other addition is to apply the IIF function to the input expression to the SQRT function. This is done to avoid negative input when using nonconstants as inputs to our numbers function, and in case the optimizer decides to handle the predicate involving SQRT before the predicate @high>=@low.

Before the IIF addition, for example, the predicate involving N1.n2 looked like this:

N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))

After adding IIF, it looks like this:

N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))

With these two additions, we’re now basically ready for the final definition of the dbo.GetNums_SQLkiwi function:

CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
        @low - 2 + N.rn < @high;
GO

Now back to the comment about the constant scan. When using constants that result in a negative range as inputs to the function, e.g., 100,000,000 and 1 as @low and @high, after parameter embedding the WHERE filter of the inner query looks like this:

WHERE
    1 >= 100000000
    AND ...

The whole plan can then be simplified to a single Constant Scan operator. Essayez-le :

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);

The plan for this execution is shown in Figure 13.

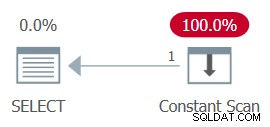Figure 13:Plan with constant scan

Unsurprisingly, I got the following performance numbers for this execution:

logical reads 0

When passing a negative range with nonconstants as inputs, the use of the IIF function will prevent any attempt to compute a square root of a negative input.

Now let’s test the function with a valid input range:

SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);

You get the all-batch-mode plan shown in Figure 14.

Figure 14:Plan for dbo.GetNums_SQLkiwi function

This is the same plan you saw earlier in Figure 7.

I got the following time statistics for this execution:

Ladies and gentlemen, I think we have a winner! :)

Conclusion

I’ll have what Paul’s having.

Are we done yet, or is this series going to last forever?

No and no.