Seuils d'optimisation – Regroupement et agrégation de données, partie 2

Cet article est le deuxième d'une série sur les seuils d'optimisation liés au regroupement et à l'agrégation des données. Dans la partie 1, j'ai fourni la formule de rétro-ingénierie pour le coût de l'opérateur Stream Aggregate. J'ai expliqué que cet opérateur doit consommer les lignes ordonnées par l'ensemble de regroupement (n'importe quel ordre de ses membres), et que lorsque les données sont obtenues préordonnées à partir d'un index, vous obtenez une mise à l'échelle linéaire par rapport au nombre de lignes et au nombre de groupes. De plus, aucune allocation de mémoire n'est nécessaire dans un tel cas.

Dans cet article, je me concentre sur le coût et la mise à l'échelle d'une opération basée sur l'agrégation de flux lorsque les données ne sont pas obtenues pré-ordonnées à partir d'un index, mais doivent plutôt être triées en premier.

Dans mes exemples, j'utiliserai l'exemple de base de données PerformanceV3, comme dans la partie 1. Vous pouvez télécharger le script qui crée et remplit cette base de données à partir d'ici. Avant d'exécuter les exemples de cet article, assurez-vous d'exécuter d'abord le code suivant pour supprimer quelques index inutiles :

SUPPRIMER L'INDEX idx_nc_sid_od_cid SUR dbo.Orders ;SUPPRIMER L'INDEX idx_unc_od_oid_i_cid_eid SUR dbo.Orders ;

Les deux seuls index qui doivent rester sur cette table sont idx_cl_od (regroupé avec orderdate comme clé) et PK_Orders (non clusterisé avec orderid comme clé).

Trier + Agréger de flux

L'objectif de cet article est d'essayer de comprendre comment une opération d'agrégation de flux évolue lorsque les données ne sont pas préordonnées par l'ensemble de regroupement. Étant donné que l'opérateur Stream Aggregate doit traiter les lignes triées, si elles ne sont pas pré-ordonnées dans un index, le plan doit inclure un opérateur Sort explicite. Ainsi, le coût de l'opération d'agrégation à prendre en compte est la somme des coûts des opérateurs Sort + Stream Aggregate.

J'utiliserai la requête suivante (que nous appellerons la requête 1) pour démontrer un plan impliquant une telle optimisation :

SELECT shipperid, MAX(orderdate) AS maxod FROM (SELECT TOP (100) * FROM dbo.Orders) AS D GROUP BY shipperid ;

Le plan de cette requête est illustré à la figure 1.

Figure 1 :Plan pour la requête 1

La raison pour laquelle j'utilise une expression de table avec un filtre TOP est de contrôler le nombre exact de lignes (estimées) impliquées dans le regroupement et l'agrégation. L'application de modifications contrôlées facilite la rétro-ingénierie des formules d'établissement des coûts.

Si vous vous demandez pourquoi filtrer un si petit nombre de lignes dans cet exemple, cela a à voir avec les seuils d'optimisation qui font que cette stratégie est préférée à l'algorithme Hash Aggregate. Dans la partie 3, je décrirai le coût et la mise à l'échelle de l'alternative de hachage. Dans les cas où l'optimiseur ne choisit pas lui-même une opération d'agrégation de flux, par exemple lorsqu'un grand nombre de lignes sont impliquées, vous pouvez toujours la forcer avec l'indication OPTION(ORDER GROUP) pendant le processus de recherche. Lorsque vous vous concentrez sur le coût des plans en série, vous pouvez évidemment ajouter un indice MAXDOP 1 pour éliminer le parallélisme.

Comme mentionné, pour évaluer le coût et la mise à l'échelle d'un algorithme d'agrégation de flux non préordonné, vous devez prendre en compte la somme des opérateurs Sort + Stream Aggregate. Vous connaissez déjà la formule de calcul des coûts pour l'opérateur Stream Aggregate de la partie 1 :

@numrows * 0.0000006 + @numgroups * 0.0000005

Dans notre requête, nous avons 100 lignes d'entrée estimées et 5 groupes de sortie estimés (5 ID d'expéditeur distincts estimés sur la base des informations de densité). Ainsi, le coût de l'opérateur Stream Aggregate dans notre plan est :

100 * 0,0000006 + 5 * 0,0000005 =0,0000625

Essayons de comprendre la formule de coût pour l'opérateur de tri. N'oubliez pas que nous nous concentrons sur le coût estimé et la mise à l'échelle, car notre objectif ultime est de déterminer les seuils d'optimisation où l'optimiseur modifie ses choix d'une stratégie à l'autre.

L'estimation du coût des E/S semble être fixe :0,0112613. J'obtiens le même coût d'E/S indépendamment de facteurs tels que le nombre de lignes, le nombre de colonnes de tri, le type de données, etc. Cela est probablement dû à certains travaux d'E/S prévus.

En ce qui concerne le coût du processeur, hélas, Microsoft n'expose pas publiquement les algorithmes exacts qu'ils utilisent pour le tri. Cependant, parmi les algorithmes courants utilisés pour le tri par les moteurs de base de données en général, il existe différentes implémentations du tri par fusion et du tri rapide. Grâce aux efforts de Paul White, qui aime regarder les traces de la pile du débogueur Windows (nous n'avons pas tous l'estomac pour cela), nous avons un peu plus d'informations sur le sujet, publié dans sa série "Internals of the Seven SQL Server Trie. Selon les découvertes de Paul, la classe de tri générale (utilisée dans le plan ci-dessus) utilise le tri par fusion (d'abord interne, puis passe à externe). En moyenne, cet algorithme nécessite n log n comparaisons pour trier n éléments. Dans cet esprit, il est probablement plus sûr comme point de départ de supposer que la partie CPU du coût de l'opérateur est basée sur une formule telle que :

Coût CPU de l'opérateur = + @numrows * LOG(@numrows) *

Bien sûr, cela pourrait être une simplification excessive de la formule de coût réel utilisée par Microsoft, mais en l'absence de documentation à ce sujet, il s'agit d'une première estimation.

Ensuite, vous pouvez obtenir les coûts de tri CPU à partir de deux plans de requête produits pour trier différents nombres de lignes, disons 1000 et 2000, et sur la base de ceux-ci et de la formule ci-dessus, procéder à l'ingénierie inverse du coût de comparaison et du coût de démarrage. Pour cela, vous n'avez pas besoin d'utiliser une requête groupée ; il suffit de faire un simple ORDER BY. Je vais utiliser les deux requêtes suivantes (nous les appellerons requête 2 et requête 3) :

SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (1000) * FROM dbo.Orders) AS D ORDER BY myorderid; SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (2000) * FROM dbo.Orders) AS D ORDER BY myorderid;

L'intérêt du tri selon le résultat d'un calcul est de forcer l'utilisation d'un opérateur de tri dans le plan.

La figure 2 montre les parties pertinentes des deux plans :

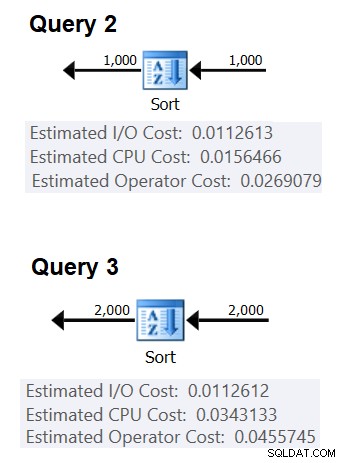
Figure 2 :Plans pour les requêtes 2 et 3

Pour essayer de déduire le coût d'une comparaison, vous utiliseriez la formule suivante :

coût de comparaison =

(( – ) – ( – ))

/ ( – ) =

(0.0343133 – 0.0156466) / (2000*LOG(2000) – 1000*LOG(1000)) =2.25061348918698E-06

En ce qui concerne le coût de démarrage, vous pouvez le déduire en fonction de l'un ou l'autre des plans, par exemple, en fonction du plan qui trie 2 000 lignes :

coût de démarrage = – #comparisons * =

0,0343133 – 2000*LOG(2000) * 2,25061348918698E-06 =9,99127891201865E-05

Et ainsi notre formule de coût CPU de tri devient :

Coût CPU de l'opérateur de tri =9,99127891201865E-05 + @numrows * LOG(@numrows) * 2,25061348918698E-06

En utilisant des techniques similaires, vous constaterez que des facteurs tels que la taille moyenne des lignes, le nombre de colonnes de classement et leurs types de données n'affectent pas le coût estimé du processeur de tri. Le seul facteur qui semble être pertinent est le nombre estimé de lignes. Notez que le tri nécessitera une allocation de mémoire, et l'allocation est proportionnelle au nombre de lignes (pas de groupes) et à la taille moyenne des lignes. Mais nous nous concentrons actuellement sur le coût estimé de l'opérateur, et il semble que cette estimation ne soit affectée que par le nombre estimé de lignes.

Cette formule semble bien prédire le coût du processeur jusqu'à un seuil d'environ 5 000 lignes. Essayez avec les nombres suivants :100, 200, 300, 400, 500, 1000, 2000, 3000, 4000, 5000 :

SELECT numrows, 9.99127891201865E-05 + numrows * LOG(numrows) * 2.25061348918698E-06 AS predicatedcost FROM (VALUES(100), (200), (300), (400), (500), (1000) , (2000), (3000), (4000), (5000)) AS D(numrows);

Comparez ce que la formule prédit et les coûts CPU estimés que les plans affichent pour les requêtes suivantes :

SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (100) * FROM dbo.Orders) AS D ORDER BY myorderid; SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (200) * FROM dbo.Orders) AS D ORDER BY myorderid; SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (300) * FROM dbo.Orders) AS D ORDER BY myorderid; SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (400) * FROM dbo.Orders) AS D ORDER BY myorderid; SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (500) * FROM dbo.Orders) AS D ORDER BY myorderid; SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (1000) * FROM dbo.Orders) AS D ORDER BY myorderid; SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (2000) * FROM dbo.Orders) AS D ORDER BY myorderid; SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (3000) * FROM dbo.Orders) AS D ORDER BY myorderid; SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (4000) * FROM dbo.Orders) AS D ORDER BY myorderid; SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (5000) * FROM dbo.Orders) AS D ORDER BY myorderid;

J'ai obtenu les résultats suivants :

 numrows predicatedcost estimatecost ratio ----------- --------------- -------------- --- ---- 100 0.0011363 0.0011365 1.00018 200 0.0024848 0.0024849 1.00004 300 0.0039510 0.0039511 1.00003 400 0.0054937 0.0054938 1.00002 500 0.0070933 0.0070933 1.00000 1000 0.0156466 0.0156466 1.00000 2000 0.0343133 0.0343133 1.00000 3000 0.0541576 0.0541576 1.00000 4000 0.0747667 0.0747665  1.00000 5000 0.0959445 0.0959442 1.00000

La colonne predictedcost montre la prédiction basée sur notre formule de rétro-ingénierie, la colonne estimatecost montre le coût estimé qui apparaît dans le plan, et la colonne ratio montre le rapport entre ce dernier et le premier.

La prédiction semble assez précise jusqu'à 5 000 lignes. Cependant, avec des nombres supérieurs à 5 000, notre formule de rétro-ingénierie cesse de bien fonctionner. La requête suivante vous donne les prédictions pour les lignes 6K, 7K, 10K, 20K, 100K et 200K :

SELECT numrows, 9.99127891201865E-05 + numrows * LOG(numrows) * 2.25061348918698E-06 AS predicatedcost FROM (VALUES(6000), (7000), (10000), (20000), (100000), (200000) ) AS D(numrows);

Utilisez les requêtes suivantes pour obtenir les coûts CPU estimés à partir des plans (notez l'astuce pour forcer un plan en série car avec un plus grand nombre de lignes, il est plus probable que vous obteniez un plan parallèle où les formules de coût sont ajustées pour le parallélisme) :

SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (6000) * FROM dbo.Orders) AS D ORDER BY myorderid OPTION(MAXDOP 1); SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (7000) * FROM dbo.Orders) AS D ORDER BY myorderid OPTION(MAXDOP 1); SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (10000) * FROM dbo.Orders) AS D ORDER BY myorderid OPTION(MAXDOP 1); SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (20000) * FROM dbo.Orders) AS D ORDER BY myorderid OPTION(MAXDOP 1); SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D ORDER BY myorderid OPTION(MAXDOP 1); SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (200000) * FROM dbo.Orders) AS D ORDER BY myorderid OPTION(MAXDOP 1);

J'ai obtenu les résultats suivants :

numrows predicatedcost estimatecost ratio ----------- --------------- -------------- --- --- 6000 0.117575 0.160970 1.3691 7000 0.139583 0,244848 1,7541 10000 0,207389 0,603420 2.9096 20000 0,445878 1.311710 2,9419 100000 2,591210 7,623920

Comme vous pouvez le voir, au-delà de 5 000 lignes notre formule devient de moins en moins précise, mais curieusement, le taux de précision se stabilise sur environ 2,94 à environ 20 000 lignes. Cela implique qu'avec de grands nombres, notre formule s'applique toujours, uniquement avec un coût de comparaison plus élevé, et qu'environ entre 5 000 et 20 000 lignes, elle passe progressivement du coût de comparaison le plus bas au plus élevé. Mais qu'est-ce qui pourrait expliquer la différence entre la petite et la grande échelle ? La bonne nouvelle est que la réponse n'est pas aussi complexe que de concilier la mécanique quantique et la relativité générale avec la théorie des cordes. C'est juste qu'à plus petite échelle, Microsoft voulait tenir compte du fait que le cache du processeur est susceptible d'être utilisé, et pour des raisons de coût, ils supposent une taille de cache fixe.

Ainsi, pour déterminer le coût de comparaison à grande échelle, vous souhaitez utiliser le tri des coûts CPU de deux plans pour les nombres supérieurs à 20 000. J'utiliserai 100 000 et 200 000 lignes (les deux dernières lignes du tableau ci-dessus). Voici la formule pour déduire le coût de comparaison :

coût de comparaison =

(16,1657 – 7,62392) / (200000*LOG(200000) – 100000*LOG(100000)) =6,62193536908588E-06

Ensuite, voici la formule pour déduire le coût de démarrage basé sur le plan pour 200 000 lignes :

coût de démarrage =

16,1657 – 200000*LOG(200000) * 6,62193536908588E-06 =1,35166186417734E-04

Il se pourrait très bien que le coût de démarrage pour les petites et les grandes échelles soit le même, et que la différence que nous avons obtenue soit due à des erreurs d'arrondi. Quoi qu'il en soit, avec un grand nombre de lignes, le coût de démarrage devient négligeable par rapport au coût des comparaisons.

En résumé, voici la formule du coût CPU de l'opérateur de tri pour les grands nombres (>=20000) :

Coût CPU de l'opérateur =1,35166186417734E-04 + @numrows * LOG(@numrows) * 6,62193536908588E-06

Testons la précision de la formule avec des lignes de 500K, 1M et 10M. Le code suivant vous donne les prédications de notre formule :

SELECT numrows, 1.35166186417734E-04 + numrows * LOG(numrows) * 6.62193536908588E-06 AS predicatedcost FROM (VALUES(500000), (1000000), (10000000)) AS D(numrows);

Utilisez les requêtes suivantes pour obtenir les coûts CPU estimés :

SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (500000) * FROM dbo.Orders) AS D ORDER BY myorderid OPTION(MAXDOP 1); SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (1000000) * FROM dbo.Orders) AS D ORDER BY myorderid OPTION(MAXDOP 1); SELECT CHECKSUM(NEWID()) as myorderid FROM (SELECT TOP (10000000) O1.orderid FROM dbo.Orders AS O1 CROSS JOIN dbo.Orders AS O2) AS D ORDER BY myorderid OPTION(MAXDOP 1);

J'ai obtenu les résultats suivants :

 numrows predicatedcost estimatecost ratio ----------- --------------- -------------- --- --- 500000 43.4479 43.448 1.0000 1000000 91.4856 91.486 1.0000 10000000 1067.3300 1067.340 1.0000

Il semble que notre formule pour les grands nombres fonctionne plutôt bien.

Tout mettre ensemble

Le coût total de l'application d'un agrégat de flux avec tri explicite pour un petit nombre de lignes (<= 5 000 lignes) est :

+ + =

0,0112613

+ 9,99127891201865E-05 + @numrows * LOG(@ numrows) * 2.25061348918698E-06

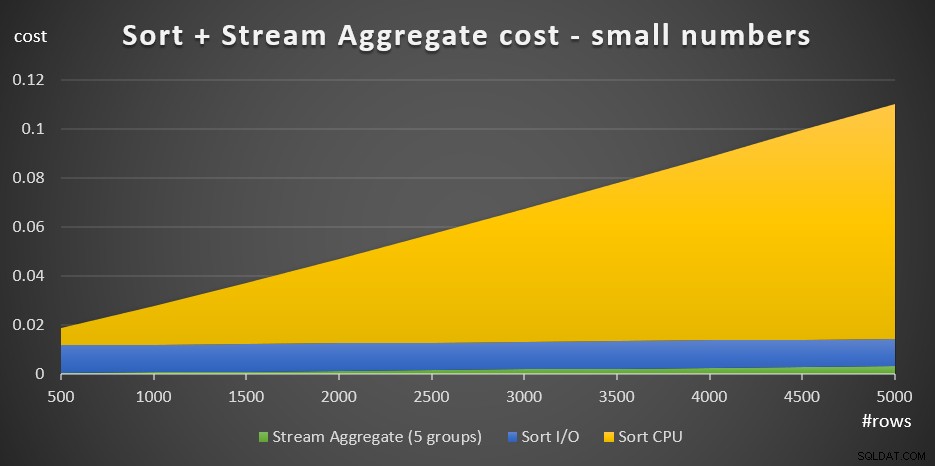
+ @numrows * 0.0000006 + @numgroups * 0.0000005

La figure 3 présente un graphique en aires montrant comment ce coût évolue.

Figure 3 :coût du tri + agrégat de flux pour un petit nombre de lignes

Le coût de l'unité centrale de tri est la partie la plus importante du coût total de l'agrégat Tri + Flux. Néanmoins, avec un petit nombre de lignes, le coût de Stream Aggregate et la partie Sort I/O du coût ne sont pas entièrement négligeables. En termes visuels, vous pouvez clairement voir les trois parties dans le graphique.

Comme pour un grand nombre de lignes (>=20 000), la formule de coût est la suivante :

0,0112613

+ 1,35166186417734E-04 + @numrows * LOG(@numrows) * 6,62193536908588E-06

+ @numrows * 0,0000006 + @numgroups * 0,0000005

Je n'ai pas vu beaucoup d'intérêt à rechercher la manière exacte dont les coûts de comparaison passent de la petite à la grande échelle.

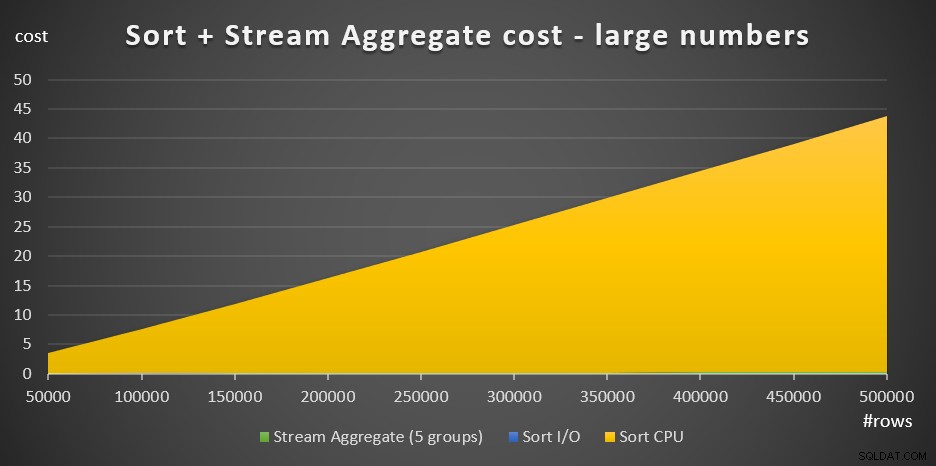
La figure 4 présente un graphique en aires montrant comment le coût évolue pour de grands nombres.

Figure 4 :coût du tri + agrégat de flux pour un grand nombre de lignes

Avec un grand nombre de lignes, le coût d'agrégation de flux et le coût d'E/S de tri sont si négligeables par rapport au coût CPU de tri qu'ils ne sont même pas visibles à l'œil nu dans le graphique. De plus, la part du coût du processeur de tri attribuée au travail de démarrage est également négligeable. Par conséquent, la seule partie du calcul des coûts qui est vraiment significative est le coût total de comparaison :

@numrows * LOG(@numrows) *

Cela signifie que lorsque vous devez évaluer la mise à l'échelle de la stratégie Sort + Stream Aggregate, vous pouvez la simplifier à cette seule partie dominante. Par exemple, si vous avez besoin d'évaluer comment le coût passerait de 100 000 lignes à 100 000 000 lignes, vous pouvez utiliser la formule (notez que le coût de comparaison n'est pas pertinent) :

(100000000 * LOG(100000000) * ) / (100000 * LOG(100000) * ) =1600

Cela vous indique que lorsque le nombre de lignes passe de 100 000 par un facteur de 1 000 à 100 000 000, le coût estimé augmente par un facteur de 1 600.

La mise à l'échelle de 1 000 000 à 1 000 000 000 de lignes est calculée comme suit :

(1000000000 * LOG(1000000000)) / (1000000 * LOG(1000000)) =1500

Autrement dit, lorsque le nombre de lignes augmente d'un facteur de 1 000 à partir de 1 000 000, le coût estimé augmente d'un facteur de 1 500.

Ce sont des observations intéressantes sur la façon dont la stratégie Sort + Stream Aggregate évolue. En raison de son coût de démarrage très faible et de sa mise à l'échelle linéaire supplémentaire, vous vous attendez à ce que cette stratégie fonctionne bien avec un très petit nombre de lignes, mais pas aussi bien avec un grand nombre. De plus, le fait que l'opérateur Stream Aggregate représente à lui seul une si petite fraction du coût par rapport au moment où un tri est également nécessaire, vous indique que vous pouvez obtenir des performances nettement meilleures si la situation est telle que vous êtes en mesure de créer un index de support. .

Dans la prochaine partie de la série, je couvrirai la mise à l'échelle de l'algorithme Hash Aggregate. Si vous aimez cet exercice consistant à essayer de trouver des formules de coût, voyez si vous pouvez le comprendre pour cet algorithme. Ce qui est important, c'est de comprendre les facteurs qui l'affectent, la façon dont il évolue et les conditions dans lesquelles il fonctionne mieux que les autres algorithmes.