Dans cet article, je poursuis la couverture des solutions au défi alléchant de Peter Larsson en matière d'adéquation entre l'offre et la demande. Merci encore à Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie et Peter Larsson, pour l'envoi de vos solutions.
Le mois dernier, j'ai couvert une solution basée sur des intersections d'intervalles, en utilisant un test classique d'intersection d'intervalles basé sur des prédicats. J'appellerai cette solution des intersections classiques . L'approche classique des intersections d'intervalles donne un plan avec une échelle quadratique (N^2). J'ai démontré ses mauvaises performances par rapport à des entrées d'échantillons allant de 100 000 à 400 000 lignes. Il a fallu 931 secondes à la solution par rapport à l'entrée de 400 000 lignes ! Ce mois-ci, je commencerai par vous rappeler brièvement la solution du mois dernier et pourquoi elle évolue et fonctionne si mal. Je présenterai ensuite une approche basée sur une révision du test d'intersection d'intervalle. Cette approche a été utilisée par Luca, Kamil et peut-être aussi Daniel, et elle permet une solution avec des performances et une mise à l'échelle bien meilleures. J'appellerai cette solution intersections révisées .
Le problème avec le test d'intersection classique
Commençons par un petit rappel de la solution du mois dernier.
J'ai utilisé les index suivants sur la table d'entrée dbo.Auctions pour prendre en charge le calcul des totaux cumulés qui produisent les intervalles de demande et d'approvisionnement :
-- Index to support solution CREATE UNIQUE NONCLUSTERED INDEX idx_Code_ID_i_Quantity ON dbo.Auctions(Code, ID) INCLUDE(Quantity); -- Enable batch-mode Window Aggregate CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs ON dbo.Auctions(ID) WHERE ID = -1 AND ID = -2;
Le code suivant contient la solution complète implémentant l'approche classique des intersections d'intervalle :
-- Drop temp tables if exist
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
WITH D0 AS
-- D0 computes running demand as EndDemand
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
FROM dbo.Auctions
WHERE Code = 'D'
),
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
D AS
(
SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
FROM D0
)
SELECT ID,
CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
WITH S0 AS
-- S0 computes running supply as EndSupply
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
FROM dbo.Auctions
WHERE Code = 'S'
),
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
S AS
(
SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
FROM S0
)
SELECT ID,
CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
CREATE UNIQUE CLUSTERED INDEX idx_cl_ES_ID ON #Supply(EndSupply, ID);
-- Trades are the overlapping segments of the intersecting intervals
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
INNER JOIN #Supply AS S WITH (FORCESEEK)
ON D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply; Ce code commence par calculer les intervalles de demande et d'approvisionnement et les écrit dans des tables temporaires appelées #Demand et #Supply. Le code crée ensuite un index clusterisé sur #Supply avec EndSupply comme clé principale pour prendre en charge au mieux le test d'intersection. Enfin, le code joint #Supply et #Demand, identifiant les échanges comme les segments qui se chevauchent des intervalles qui se croisent, en utilisant le prédicat de jointure suivant basé sur le test d'intersection d'intervalle classique :
D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply
Le plan de cette solution est illustré à la figure 1.
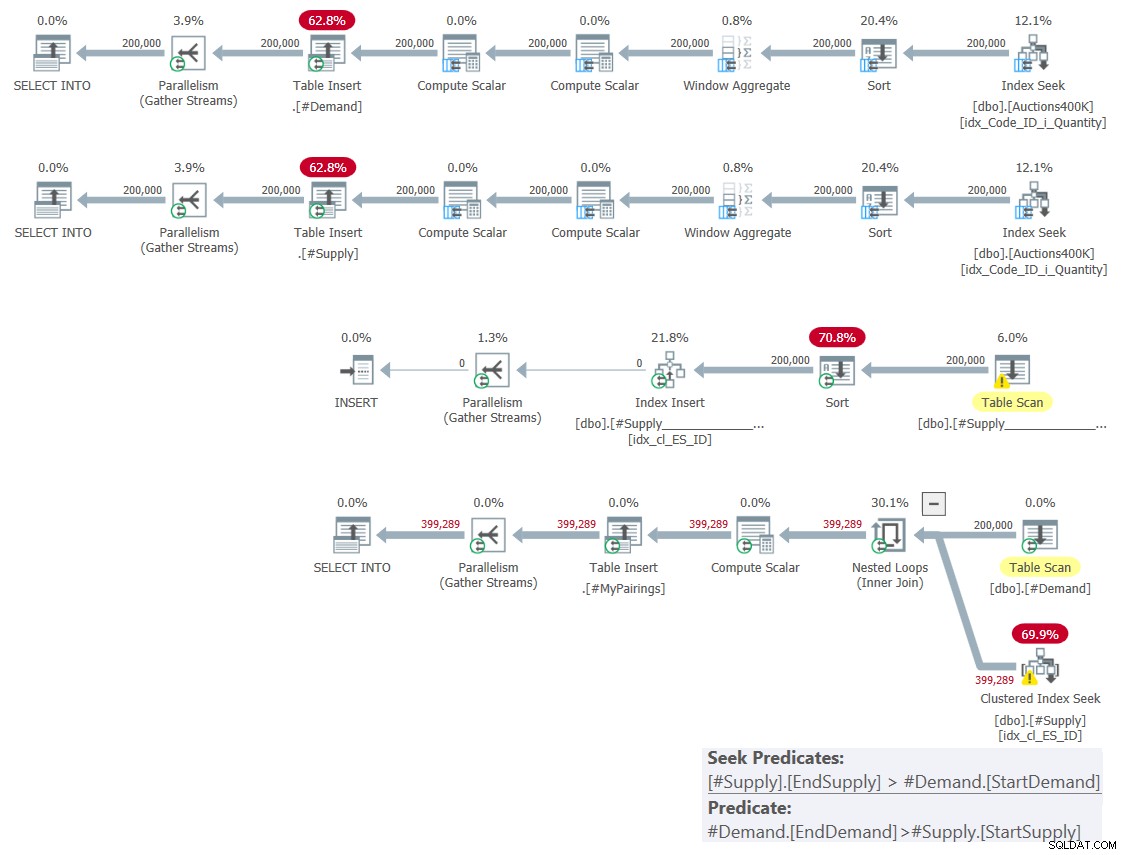 Figure 1 :Plan de requête pour une solution basée sur des intersections classiques
Figure 1 :Plan de requête pour une solution basée sur des intersections classiques
Comme je l'ai expliqué le mois dernier, parmi les deux prédicats de plage impliqués, un seul peut être utilisé comme prédicat de recherche dans le cadre d'une opération de recherche d'index, tandis que l'autre doit être appliqué comme prédicat résiduel. Vous pouvez clairement le voir dans le plan de la dernière requête de la figure 1. C'est pourquoi je n'ai pris la peine de créer qu'un seul index sur l'une des tables. J'ai également forcé l'utilisation d'une recherche dans l'index que j'ai créé à l'aide de l'indice FORCESEEK. Sinon, l'optimiseur pourrait finir par ignorer cet index et en créer un à l'aide d'un opérateur Index Spool.
Ce plan a une complexité quadratique puisque par ligne d'un côté — #Demand dans notre cas — l'index seek devra accéder en moyenne à la moitié des lignes de l'autre côté — #Supply dans notre cas — en fonction du prédicat seek, et identifier le correspondances finales en appliquant le prédicat résiduel.
Si vous ne comprenez toujours pas pourquoi ce plan a une complexité quadratique, peut-être qu'une représentation visuelle du travail pourrait vous aider, comme le montre la figure 2.
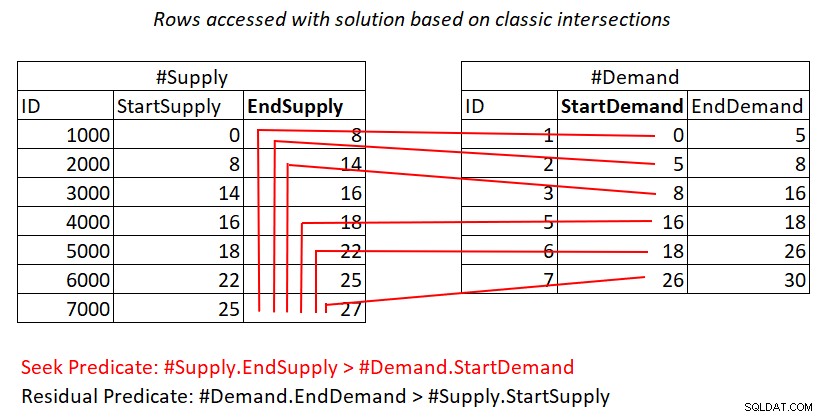 Figure 2 :Illustration du travail avec une solution basée sur des intersections classiques
Figure 2 :Illustration du travail avec une solution basée sur des intersections classiques
Cette illustration représente le travail effectué par la jointure Nested Loops dans le plan pour la dernière requête. Le tas #Demand est l'entrée externe de la jointure et l'index clusterisé sur #Supply (avec EndSupply comme clé principale) est l'entrée interne. Les lignes rouges représentent les activités de recherche d'index effectuées par ligne dans #Demand dans l'index sur #Supply et les lignes auxquelles elles accèdent dans le cadre des analyses de plage dans la feuille d'index. Vers des valeurs StartDemand extrêmement basses dans #Demand, l'analyse de plage doit accéder à près de toutes les lignes dans #Supply. Vers des valeurs StartDemand extrêmement élevées dans #Demand, l'analyse de plage doit accéder à des lignes proches de zéro dans #Supply. En moyenne, l'analyse de gamme doit accéder à environ la moitié des lignes de #Supply par ligne en demande. Avec D lignes demande et S lignes offre, le nombre de lignes accédées est D + D*S/2. Cela s'ajoute au coût des recherches qui vous amènent aux lignes correspondantes. Par exemple, lorsque vous remplissez dbo.Auctions avec 200 000 lignes de demande et 200 000 lignes d'approvisionnement, cela se traduit par l'accès à 200 000 lignes de demande + 200 000 * 200 000/2 lignes d'approvisionnement, ou 200 000 + 200 000^2/2 =20 000 200 000 lignes accessibles. Il y a beaucoup de renumérisation des rangées d'approvisionnement ici !
Si vous voulez vous en tenir à l'idée des intersections d'intervalle mais obtenir de bonnes performances, vous devez trouver un moyen de réduire la quantité de travail effectué.
Dans sa solution, Joe Obbish a compartimenté les intervalles en fonction de la longueur d'intervalle maximale. De cette façon, il a pu réduire le nombre de lignes que les jointures devaient gérer et s'appuyer sur le traitement par lots. Il a utilisé le test d'intersection d'intervalle classique comme filtre final. La solution de Joe fonctionne bien tant que la longueur maximale de l'intervalle n'est pas très élevée, mais le temps d'exécution de la solution augmente à mesure que la longueur maximale de l'intervalle augmente.
Alors, que pouvez-vous faire d'autre… ?
Test d'intersection révisé
Luca, Kamil et peut-être Daniel (il y avait une partie peu claire de sa solution publiée en raison du formatage du site Web, donc j'ai dû deviner) ont utilisé un test d'intersection d'intervalle révisé qui permet une bien meilleure utilisation de l'indexation.
Leur test d'intersection est une disjonction de deux prédicats (prédicats séparés par l'opérateur OU) :
(D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >= D.StartDemand AND S.StartSupply < D.EndDemand)
En anglais, soit le délimiteur de début de demande croise l'intervalle d'approvisionnement de manière inclusive et exclusive (y compris le début et excluant la fin) ; ou le délimiteur de début d'approvisionnement croise l'intervalle de demande, de manière inclusive et exclusive. Pour rendre les deux prédicats disjoints (ne pas avoir de cas qui se chevauchent) tout en restant complets en couvrant tous les cas, vous pouvez conserver l'opérateur =dans l'un ou l'autre, par exemple :
(D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand)
Ce test d'intersection d'intervalle révisé est assez perspicace. Chacun des prédicats peut potentiellement utiliser efficacement un index. Considérez le prédicat 1 :
D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply ^^^^^^^^^^^^^ ^^^^^^^^^^^^^
En supposant que vous créez un index de couverture sur #Demand avec StartDemand comme clé principale, vous pouvez potentiellement obtenir une jointure Nested Loops en appliquant le travail illustré à la figure 3.
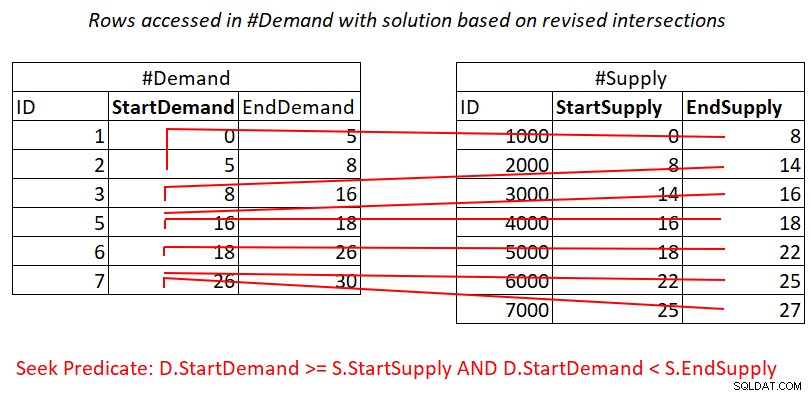
Figure 3 :Illustration du travail théorique requis pour traiter le prédicat 1
Oui, vous payez toujours pour une recherche dans l'index #Demand par ligne dans #Supply, mais les balayages de plage dans l'index feuille accèdent à des sous-ensembles de lignes presque disjoints. Pas de renumérisation des lignes !
La situation est similaire avec le prédicat 2 :
S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand ^^^^^^^^^^^^^ ^^^^^^^^^^^^^
En supposant que vous créez un index de couverture sur #Supply avec StartSupply comme clé principale, vous pouvez potentiellement obtenir une jointure Nested Loops en appliquant le travail illustré à la figure 4.
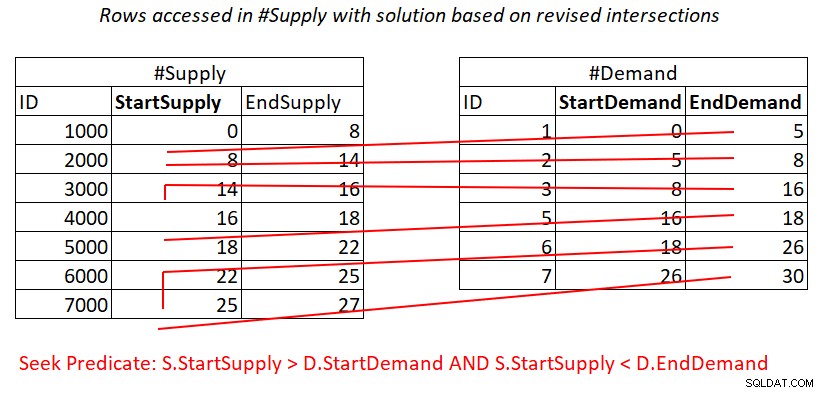
Figure 4 :Illustration du travail théorique requis pour traiter le prédicat 2
De plus, ici, vous payez pour une recherche dans l'index #Supply par ligne dans #Demand, puis les balayages de plage dans l'index feuille accèdent à des sous-ensembles de lignes presque disjoints. Encore une fois, pas de renumérisation des lignes !
En supposant D lignes de demande et S lignes d'approvisionnement, le travail peut être décrit comme :
Number of index seek operations: D + S Number of rows accessed: 2D + 2S
Il est donc probable que la plus grande partie du coût ici est le coût d'E / S impliqué dans les recherches. Mais cette partie du travail a une mise à l'échelle linéaire par rapport à la mise à l'échelle quadratique de la requête classique d'intersections d'intervalles.
Bien sûr, vous devez tenir compte du coût préliminaire de la création d'index sur les tables temporaires, qui a une mise à l'échelle n log n en raison du tri impliqué, mais vous payez cette partie comme une partie préliminaire des deux solutions.
Essayons de mettre cette théorie en pratique. Commençons par remplir les tables temporaires #Demand et #supply avec les intervalles de demande et d'offre (comme pour les intersections d'intervalles classiques) et en créant les index de support :
-- Drop temp tables if exist
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
WITH D0 AS
-- D0 computes running demand as EndDemand
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
FROM dbo.Auctions
WHERE Code = 'D'
),
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
D AS
(
SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
FROM D0
)
SELECT ID,
CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
WITH S0 AS
-- S0 computes running supply as EndSupply
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
FROM dbo.Auctions
WHERE Code = 'S'
),
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
S AS
(
SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
FROM S0
)
SELECT ID,
CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
-- Indexing
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID); Les plans de remplissage des tables temporaires et de création des index sont illustrés à la figure 5.
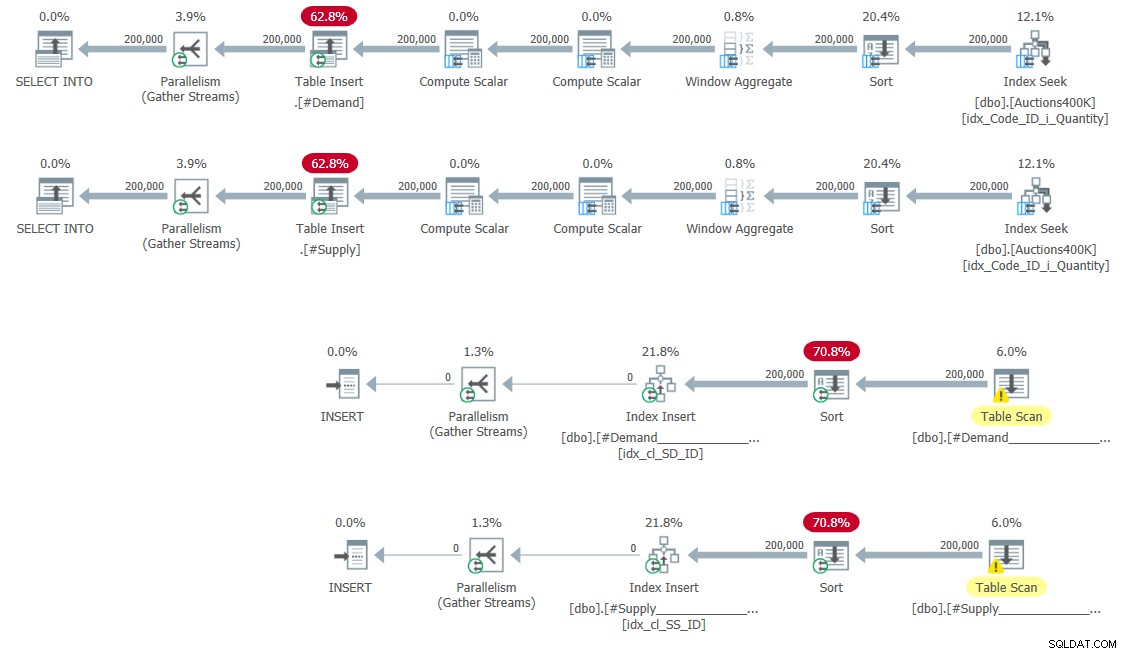
Figure 5 :Plans de requête pour remplir des tables temporaires et créer index
Pas de surprise ici.
Passons maintenant à la dernière requête. Vous pourriez être tenté d'utiliser une seule requête avec la disjonction susmentionnée de deux prédicats, comme ceci :
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
INNER JOIN #Supply AS S
ON (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand); Le plan de cette requête est illustré à la figure 6.
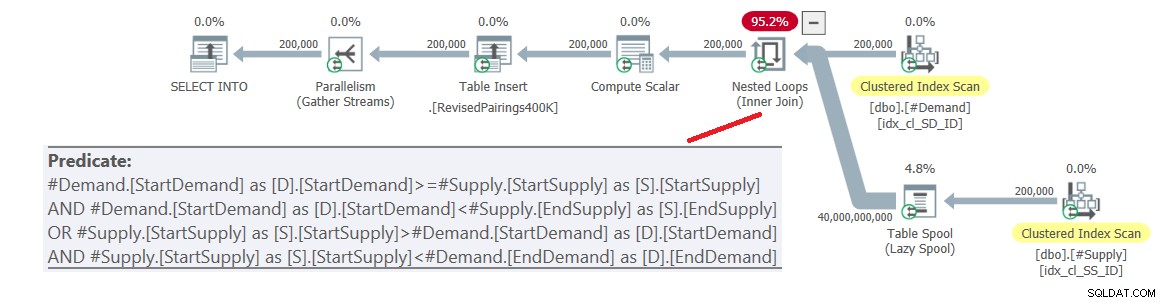
Figure 6 :Plan de requête pour la requête finale utilisant l'intersection révisée testez, essayez 1
Le problème est que l'optimiseur ne sait pas comment diviser cette logique en deux activités distinctes, chacune gérant un prédicat différent et utilisant efficacement l'index respectif. Ainsi, cela se termine par un produit cartésien complet des deux côtés, appliquant tous les prédicats comme prédicats résiduels. Avec 200 000 lignes de demande et 200 000 lignes d'approvisionnement, la jointure traite 40 000 000 000 lignes.
L'astuce perspicace utilisée par Luca, Kamil et peut-être Daniel était de diviser la logique en deux requêtes, unifiant leurs résultats. C'est là que l'utilisation de deux prédicats disjoints devient importante ! Vous pouvez utiliser un opérateur UNION ALL au lieu de UNION, ce qui évite les frais inutiles de recherche de doublons. Voici la requête implémentant cette approche :
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
INNER JOIN #Supply AS S
ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
UNION ALL
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
FROM #Demand AS D
INNER JOIN #Supply AS S
ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand; Le plan de cette requête est illustré à la figure 7.
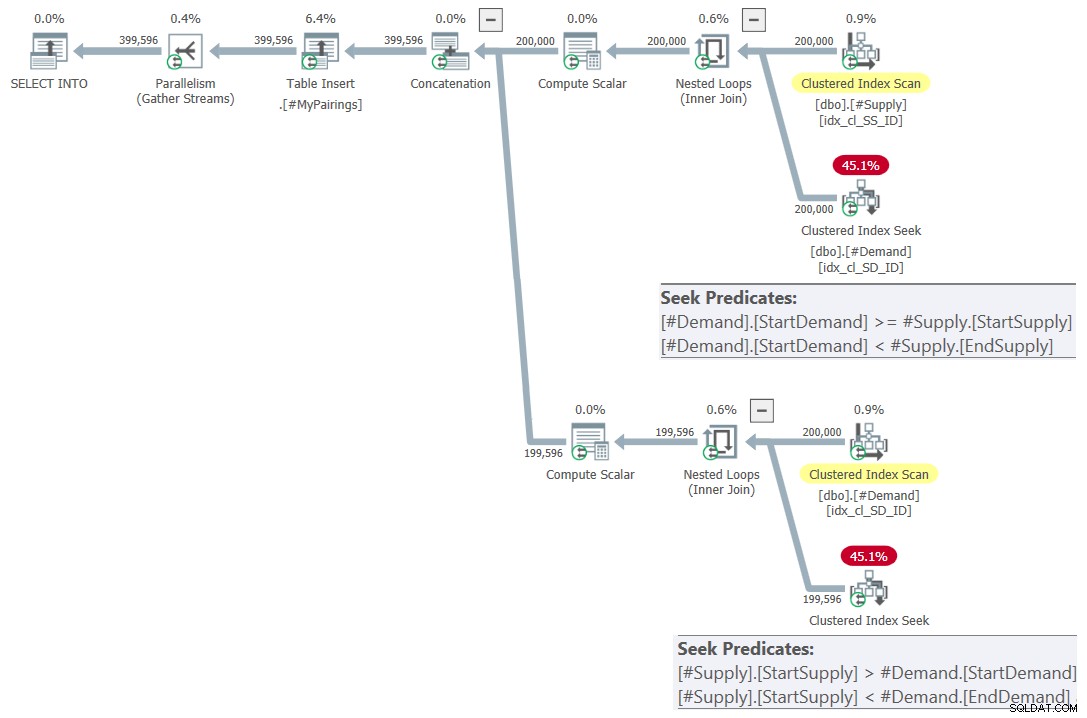
Figure 7 :Plan de requête pour la requête finale utilisant l'intersection révisée testez, essayez 2
C'est juste magnifique ! N'est-ce pas? Et parce que c'est si beau, voici la solution complète à partir de zéro, y compris la création de tables temporaires, l'indexation et la requête finale :
-- Drop temp tables if exist
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
WITH D0 AS
-- D0 computes running demand as EndDemand
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
FROM dbo.Auctions
WHERE Code = 'D'
),
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
D AS
(
SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
FROM D0
)
SELECT ID,
CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
WITH S0 AS
-- S0 computes running supply as EndSupply
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
FROM dbo.Auctions
WHERE Code = 'S'
),
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
S AS
(
SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
FROM S0
)
SELECT ID,
CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
-- Indexing
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);
-- Trades are the overlapping segments of the intersecting intervals
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
INNER JOIN #Supply AS S
ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
UNION ALL
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
FROM #Demand AS D
INNER JOIN #Supply AS S
ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand; Comme mentionné précédemment, je ferai référence à cette solution en tant que intersections révisées .
La solution de Kamil
Entre les solutions de Luca, Kamil et Daniel, celle de Kamil était la plus rapide. Voici la solution complète de Kamil :
SET NOCOUNT ON;
DROP TABLE IF EXISTS #supply, #demand;
GO
CREATE TABLE #demand
(
DemandID INT NOT NULL,
DemandQuantity DECIMAL(19, 6) NOT NULL,
QuantityFromDemand DECIMAL(19, 6) NOT NULL,
QuantityToDemand DECIMAL(19, 6) NOT NULL
);
CREATE TABLE #supply
(
SupplyID INT NOT NULL,
QuantityFromSupply DECIMAL(19, 6) NOT NULL,
QuantityToSupply DECIMAL(19,6) NOT NULL
);
WITH demand AS
(
SELECT
a.ID AS DemandID,
a.Quantity AS DemandQuantity,
SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
- a.Quantity AS QuantityFromDemand,
SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
AS QuantityToDemand
FROM dbo.Auctions AS a WHERE Code = 'D'
)
INSERT INTO #demand
(
DemandID,
DemandQuantity,
QuantityFromDemand,
QuantityToDemand
)
SELECT
d.DemandID,
d.DemandQuantity,
d.QuantityFromDemand,
d.QuantityToDemand
FROM demand AS d;
WITH supply AS
(
SELECT
a.ID AS SupplyID,
SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
- a.Quantity AS QuantityFromSupply,
SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
AS QuantityToSupply
FROM dbo.Auctions AS a WHERE Code = 'S'
)
INSERT INTO #supply
(
SupplyID,
QuantityFromSupply,
QuantityToSupply
)
SELECT
s.SupplyID,
s.QuantityFromSupply,
s.QuantityToSupply
FROM supply AS s;
CREATE UNIQUE INDEX ix_1 ON #demand(QuantityFromDemand)
INCLUDE(DemandID, DemandQuantity, QuantityToDemand);
CREATE UNIQUE INDEX ix_1 ON #supply(QuantityFromSupply)
INCLUDE(SupplyID, QuantityToSupply);
CREATE NONCLUSTERED COLUMNSTORE INDEX nci ON #demand(DemandID)
WHERE DemandID is null;
DROP TABLE IF EXISTS #myPairings;
CREATE TABLE #myPairings
(
DemandID INT NOT NULL,
SupplyID INT NOT NULL,
TradeQuantity DECIMAL(19, 6) NOT NULL
);
INSERT INTO #myPairings(DemandID, SupplyID, TradeQuantity)
SELECT
d.DemandID,
s.SupplyID,
d.DemandQuantity
- CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply
THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 end
- CASE WHEN s.QuantityToSupply < d.QuantityToDemand
THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
FROM #demand AS d
INNER JOIN #supply AS s
ON (d.QuantityFromDemand < s.QuantityToSupply
AND s.QuantityFromSupply <= d.QuantityFromDemand)
UNION ALL
SELECT
d.DemandID,
s.SupplyID,
d.DemandQuantity
- CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply
THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 END
- CASE WHEN s.QuantityToSupply < d.QuantityToDemand
THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
FROM #supply AS s
INNER JOIN #demand AS d
ON (s.QuantityFromSupply < d.QuantityToDemand
AND d.QuantityFromDemand < s.QuantityFromSupply); Comme vous pouvez le voir, c'est très proche de la solution d'intersections révisée que j'ai couverte.
Le plan de la requête finale dans la solution de Kamil est illustré à la figure 8.
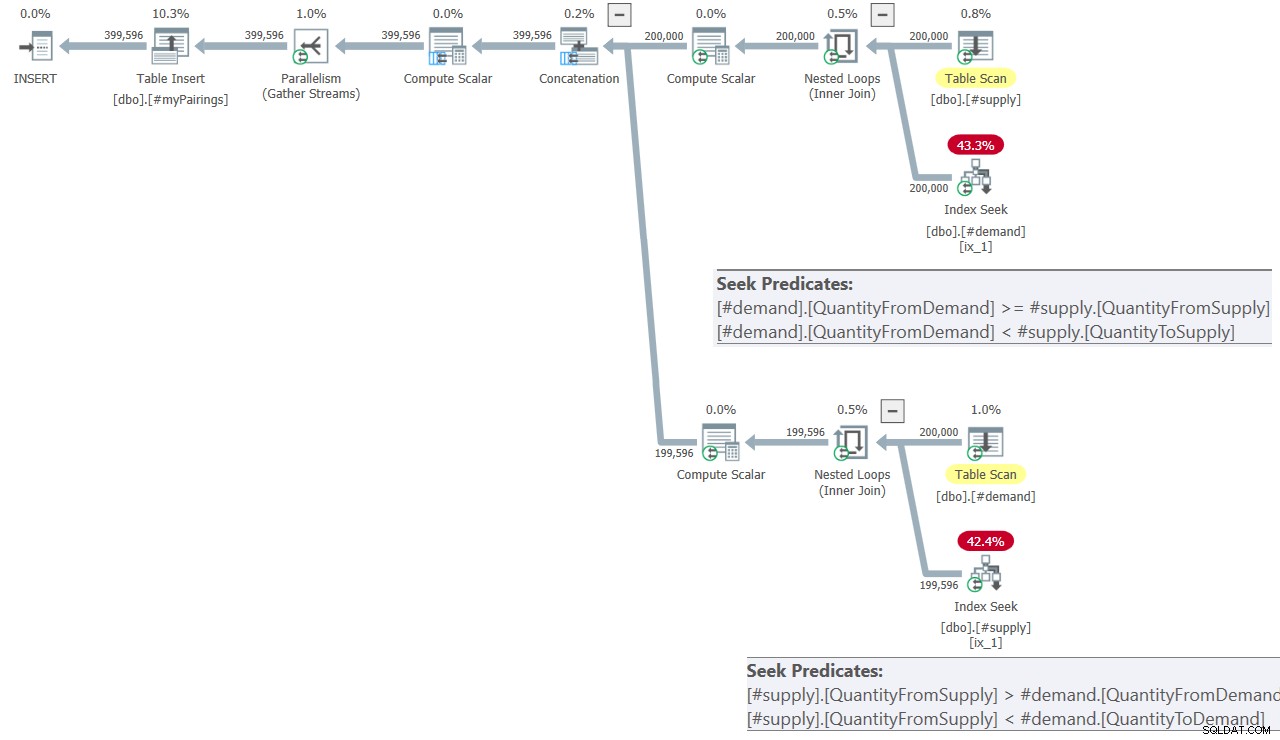
Figure 8 :Plan de requête pour la requête finale dans la solution de Kamil
Le plan est assez similaire à celui présenté précédemment dans la figure 7.
Test de performances
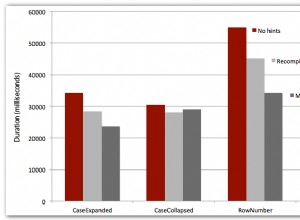
Rappelez-vous que la solution d'intersections classique a pris 931 secondes pour se terminer contre une entrée avec 400 000 lignes. C'est 15 min ! C'est bien pire que la solution du curseur, qui a pris environ 12 secondes pour se terminer avec la même entrée. La figure 9 présente les performances, y compris les nouvelles solutions décrites dans cet article.
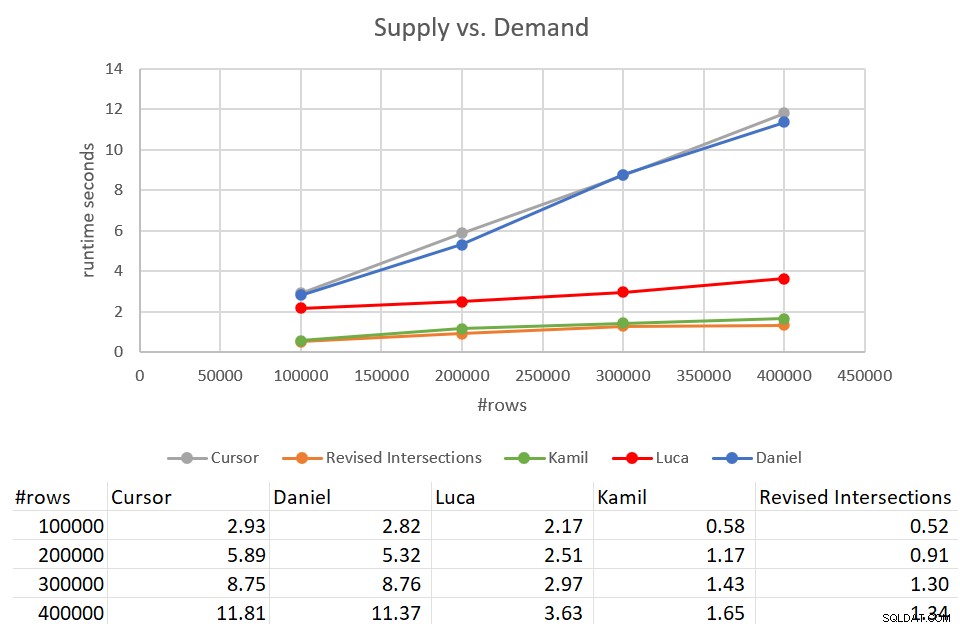
Figure 9 :Test de performances
Comme vous pouvez le voir, la solution de Kamil et la solution d'intersections révisée similaire ont pris environ 1,5 seconde pour se terminer par rapport à l'entrée de 400 000 lignes. C'est une amélioration assez décente par rapport à la solution originale basée sur le curseur. Le principal inconvénient de ces solutions est le coût des E/S. Avec une recherche par ligne, pour une entrée de 400 000 lignes, ces solutions effectuent plus de 1,35 million de lectures. Mais cela pourrait également être considéré comme un coût parfaitement acceptable compte tenu de la bonne durée d'exécution et de la mise à l'échelle que vous obtenez.
Quelle est la prochaine ?
Notre première tentative pour résoudre le défi de l'adéquation entre l'offre et la demande s'est appuyée sur le test d'intersection d'intervalle classique et a obtenu un plan peu performant avec une mise à l'échelle quadratique. Bien pire que la solution basée sur le curseur. Sur la base des informations de Luca, Kamil et Daniel, à l'aide d'un test d'intersection d'intervalle révisé, notre deuxième tentative a été une amélioration significative qui utilise l'indexation efficacement et fonctionne mieux que la solution basée sur le curseur. Cependant, cette solution implique un coût d'E/S important. Le mois prochain, je continuerai à explorer d'autres solutions.
[ Sauter vers :défi original | solutions :partie 1 | Partie 2 | Partie 3 ]