Le mois dernier, j'ai couvert le casse-tête de Peter Larsson sur l'adéquation entre l'offre et la demande. J'ai montré la solution simple basée sur le curseur de Peter et expliqué qu'elle avait une mise à l'échelle linéaire. Le défi que je vous ai laissé est d'essayer de trouver une solution basée sur un ensemble à la tâche, et mon garçon, faites en sorte que les gens relèvent le défi ! Merci Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie et, bien sûr, Peter Larsson, pour l'envoi de vos solutions. Certaines des idées étaient brillantes et carrément époustouflantes.
Ce mois-ci, je vais commencer à explorer les solutions soumises, grosso modo, en passant des moins performantes aux plus performantes. Pourquoi même s'embêter avec les moins performants ? Parce que vous pouvez encore apprendre beaucoup d'eux; par exemple, en identifiant des anti-modèles. En effet, la première tentative de résolution de ce défi pour de nombreuses personnes, y compris moi-même et Peter, est basée sur un concept d'intersection d'intervalle. Il se trouve que la technique classique basée sur les prédicats pour identifier l'intersection d'intervalle a de mauvaises performances car il n'y a pas de bon schéma d'indexation pour la prendre en charge. Cet article est dédié à cette approche peu performante. Malgré les performances médiocres, travailler sur la solution est un exercice intéressant. Cela nécessite de pratiquer l'habileté de modéliser le problème d'une manière qui se prête à un traitement basé sur des ensembles. Il est également intéressant d'identifier la raison de la mauvaise performance, ce qui permet d'éviter plus facilement l'anti-modèle à l'avenir. Gardez à l'esprit que cette solution n'est qu'un point de départ.
DDL et un petit ensemble d'exemples de données
Pour rappel, la tâche consiste à interroger une table appelée "Enchères"." Utilisez le code suivant pour créer la table et la remplir avec un petit ensemble d'exemples de données :
SUPPRIMER LA TABLE SI EXISTE dbo.Auctions ; CREATE TABLE dbo.Auctions( ID INT NOT NULL IDENTITY(1, 1) CONSTRAINT pk_Auctions PRIMARY KEY CLUSTERED, Code CHAR(1) NOT NULL CONSTRAINT ck_Auctions_Code CHECK (Code ='D' OR Code ='S'), Quantité DECIMAL(19 , 6) CONTRAINTE NON NULLE ck_Auctions_Quantity CHECK (Quantité> 0)); SET NOCOUNT ON ; SUPPRIMER DE dbo.Enchères ; SET IDENTITY_INSERT dbo.Auctions ON ; INSERT INTO dbo.Auctions(ID, Code, Quantity) VALUES (1, 'D', 5.0), (2, 'D', 3.0), (3, 'D', 8.0), (5, 'D', 2.0), (6, 'D', 8.0), (7, 'D', 4.0), (8, 'D', 2.0), (1000, 'S', 8.0), (2000, 'S', 6.0), (3000, 'S', 2.0), (4000, 'S', 2.0), (5000, 'S', 4.0), (6000, 'S', 3.0), (7000, 'S', 2.0); SET IDENTITY_INSERT dbo.Auctions OFF ;
Votre tâche consistait à créer des appariements qui correspondent aux entrées d'offre et de demande en fonction de l'ordre des ID, en les écrivant dans une table temporaire. Voici le résultat souhaité pour le petit ensemble d'exemples de données :
DemandID SupplyID TradeQuantity----------- ----------- --------------1 1000 5.0000002 1000 3.0000003 2000 6.0000003 3000 2.0000005 4000 2.0000006 5000 4.0000006 6000 3.0000006 7000 1.0000007 7000 1.000000
Le mois dernier, j'ai également fourni du code que vous pouvez utiliser pour remplir la table Auctions avec un grand ensemble d'échantillons de données, en contrôlant le nombre d'entrées d'offre et de demande ainsi que leur plage de quantités. Assurez-vous d'utiliser le code de l'article du mois dernier pour vérifier les performances des solutions.
Modélisation des données sous forme d'intervalles
Une idée intrigante qui se prête à la prise en charge de solutions basées sur des ensembles consiste à modéliser les données sous forme d'intervalles. En d'autres termes, représentez chaque entrée de demande et d'approvisionnement sous la forme d'un intervalle commençant par les quantités totales cumulées du même type (demande ou offre) jusqu'à mais excluant le courant, et se terminant par le total cumulé incluant le courant, bien sûr basé sur l'ID commande. Par exemple, en examinant le petit ensemble de données d'échantillon, la première entrée de demande (ID 1) correspond à une quantité de 5,0 et la seconde (ID 2) correspond à une quantité de 3,0. La première entrée de demande peut être représentée par l'intervalle début :0,0, fin :5,0, et la seconde par l'intervalle début :5,0, fin :8,0, etc.
De même, la première entrée d'approvisionnement (ID 1000) est pour une quantité de 8,0 et le second (ID 2000) est pour une quantité de 6,0. La première entrée d'approvisionnement peut être représentée par le début de l'intervalle :0,0, la fin :8,0 et la seconde par le début de l'intervalle :8,0, la fin :14,0, etc.
Les paires demande-offre que vous devez créer sont alors les segments qui se chevauchent des intervalles qui se croisent entre les deux types.
Ceci est probablement mieux compris avec une représentation visuelle de la modélisation par intervalles des données et du résultat souhaité, comme illustré à la figure 1.
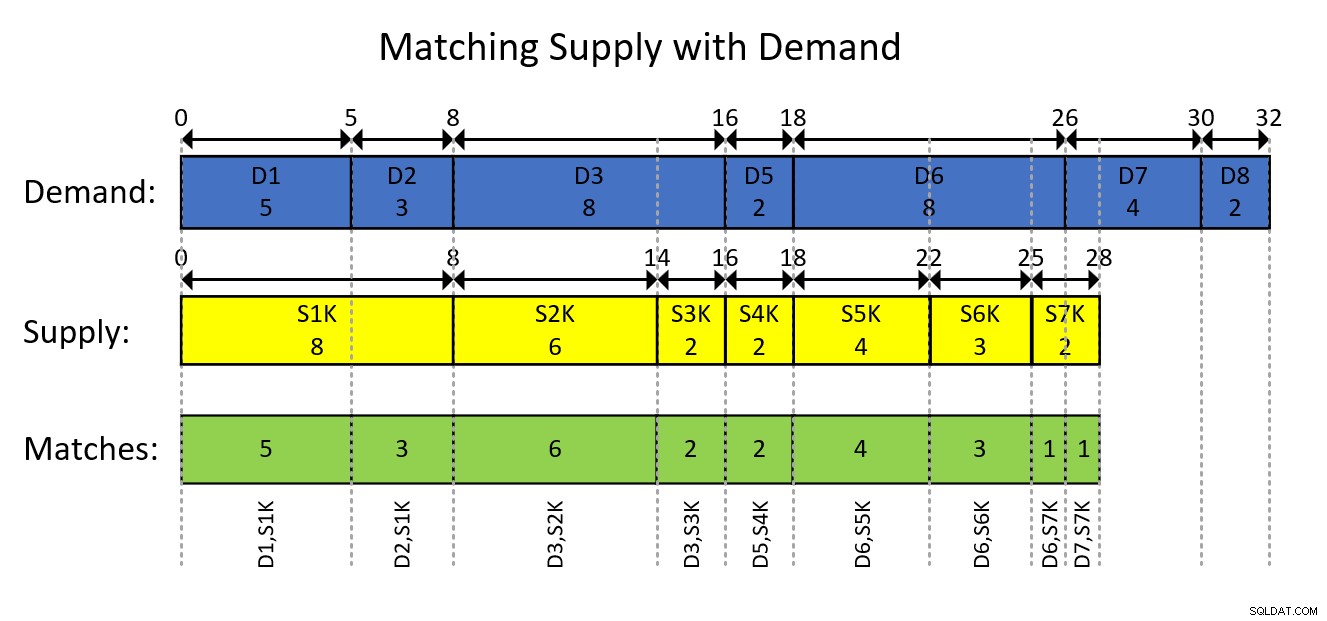Figure 1 :Modélisation des données sous forme d'intervalles
La représentation visuelle de la figure 1 est assez explicite mais, en bref…
Les rectangles bleus représentent les entrées de demande sous forme d'intervalles, indiquant les quantités totales cumulées exclusives au début de l'intervalle et le total cumulé inclusif à la fin de l'intervalle. Les rectangles jaunes font de même pour les entrées d'approvisionnement. Ensuite, remarquez comment les segments qui se chevauchent des intervalles d'intersection des deux types, qui sont représentés par les rectangles verts, sont les paires demande-offre que vous devez produire. Par exemple, le premier appariement de résultats est avec l'ID de demande 1, l'ID d'approvisionnement 1000, la quantité 5. Le deuxième appariement de résultats est avec l'ID de demande 2, l'ID d'approvisionnement 1000, la quantité 3. Et ainsi de suite.
Intersections d'intervalle à l'aide de CTE
Avant de commencer à écrire le code T-SQL avec des solutions basées sur l'idée de modélisation d'intervalle, vous devriez déjà avoir une idée intuitive des index susceptibles d'être utiles ici. Étant donné que vous utiliserez probablement des fonctions de fenêtre pour calculer les totaux cumulés, vous pourriez bénéficier d'un index de couverture avec une clé basée sur les colonnes Code, ID et incluant la colonne Quantité. Voici le code pour créer un tel index :
CRÉER UN INDEX NON CLUSTÉRÉ UNIQUE idx_Code_ID_i_Quantity ON dbo.Auctions(Code, ID) INCLUDE(Quantity);
C'est le même index que j'ai recommandé pour la solution basée sur le curseur que j'ai abordée le mois dernier.
En outre, il est possible ici de bénéficier du traitement par lots. Vous pouvez activer sa prise en compte sans les exigences du mode batch sur rowstore, par exemple, à l'aide de SQL Server 2019 Enterprise ou version ultérieure, en créant l'index factice columnstore suivant :
CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs ON dbo.Auctions(ID) WHERE ID =-1 AND ID =-2 ;
Vous pouvez maintenant commencer à travailler sur le code T-SQL de la solution.
Le code suivant crée les intervalles représentant les entrées de demande :
WITH D0 AS-- D0 calcule la demande en cours comme EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extrait prev EndDemand comme StartDemand, exprimant la demande début-fin sous la forme d'un intervalleD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0)SELECT *FROM D;
La requête définissant le CTE D0 filtre les entrées de demande de la table Auctions et calcule une quantité totale cumulée comme délimiteur de fin des intervalles de demande. Ensuite, la requête définissant le deuxième CTE appelé D interroge D0 et calcule le délimiteur de début des intervalles de demande en soustrayant la quantité actuelle du délimiteur de fin.
Ce code génère la sortie suivante :
ID Quantité StartDemand EndDemand---- --------- ------------ ----------1 5.000000 0.000000 5.0000002 3.000000 5.000000 8.0000003 8.000000 8,000000 16,0000005 2,000000 16,000000 18,0000006 8,000000 18,000000 26,0000007 4,000000 26,000000 30,0000008 2,000000Les intervalles d'approvisionnement sont générés de manière très similaire en appliquant la même logique aux entrées d'approvisionnement, en utilisant le code suivant :
WITH S0 AS-- S0 calcule l'approvisionnement en cours comme EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S extrait prev EndSupply comme StartSupply, exprimant l'approvisionnement début-fin comme un intervalleS AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)SELECT *FROM S;Ce code génère la sortie suivante :
ID Quantité StartSupply EndSupply----- --------- ------------ ----------1000 8.000000 0.000000 8.0000002000 6.000000 8.000000 14.0000003000 2.000000 14.00000016.0000004000 2.000000 16.000000 18.0000005000 4.000000 18.000000 22.0000006000 3.000000 22.000000 25.0000007000 2.000000 25.000000 27.000000Il reste alors à identifier les intervalles de demande et d'offre qui se croisent à partir des CTE D et S, et à calculer les segments qui se chevauchent de ces intervalles qui se croisent. N'oubliez pas que les paires de résultats doivent être écrites dans une table temporaire. Cela peut être fait en utilisant le code suivant :
-- Supprimez la table temporaire si elle existeDOP TABLE IF EXISTS #MyPairings ; WITH D0 AS-- D0 calcule la demande en cours comme EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extraits prev EndDemand as StartDemand, exprimant la demande début-fin sous la forme d'un intervalleD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0),S0 AS-- S0 calcule l'approvisionnement en cours comme EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER (ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S extrait prev EndSupply comme StartSupply, exprimant l'approvisionnement début-fin sous forme d'intervalleS AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)-- La requête externe identifie les échanges comme les segments qui se chevauchent des intervalles qui se croisent-- Dans les intervalles de demande et d'approvisionnement qui se croisent, la quantité de commerce est alors -- LEAST(EndDemand, EndSupply) - GREATEST(StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID AS SupplyID, CASE WH EN EndDemandStartSupply THEN StartDemand ELSE StartSupply END AS TradeQuantityINTO #MyPairingsFROM D INNER JOIN S ON D.StartDemand S.StartSupply ; Outre le code qui crée les intervalles de demande et d'offre, que vous avez déjà vu plus tôt, le principal ajout ici est la requête externe, qui identifie les intervalles d'intersection entre D et S, et calcule les segments qui se chevauchent. Pour identifier les intervalles qui se croisent, la requête externe joint D et S à l'aide du prédicat de jointure suivant :
D.StartDemandS.StartSupply C'est le prédicat classique pour identifier l'intersection d'intervalle. C'est aussi la principale source des mauvaises performances de la solution, comme je l'expliquerai bientôt.
La requête externe calcule également la quantité commerciale dans la liste SELECT comme :
LEAST(EndDemand, EndSupply) - GREATEST(StartDemand, StartSupply)Si vous utilisez Azure SQL, vous pouvez utiliser cette expression. Si vous utilisez SQL Server 2019 ou une version antérieure, vous pouvez utiliser l'alternative logiquement équivalente suivante :
CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply END Étant donné que l'exigence était d'écrire le résultat dans une table temporaire, la requête externe utilise une instruction SELECT INTO pour y parvenir.
L'idée de modéliser les données sous forme d'intervalles est clairement intrigante et élégante. Mais qu'en est-il des performances ? Malheureusement, cette solution spécifique a un gros problème lié à la façon dont l'intersection d'intervalle est identifiée. Examinez le plan de cette solution illustrée à la figure 2.
Figure 2 :Plan de requête pour les intersections à l'aide de la solution CTE
Commençons par les parties peu coûteuses du plan.
L'entrée externe de la jointure Nested Loops calcule les intervalles de demande. Il utilise un opérateur Index Seek pour récupérer les entrées de demande et un opérateur Window Aggregate en mode batch pour calculer le délimiteur de fin d'intervalle de demande (appelé Expr1005 dans ce plan). Le délimiteur de début de l'intervalle de demande est alors Expr1005 - Quantité (à partir de D).
En remarque, vous pourriez trouver l'utilisation d'un opérateur de tri explicite avant l'opérateur d'agrégation de fenêtre en mode batch surprenant ici, car les entrées de demande récupérées à partir de la recherche d'index sont déjà classées par ID comme la fonction de fenêtre en a besoin. Cela est dû au fait qu'actuellement, SQL Server ne prend pas en charge une combinaison efficace d'opérations d'index parallèles préservant l'ordre avant un opérateur Window Aggregate en mode batch parallèle. Si vous forcez un plan en série uniquement à des fins d'expérimentation, vous verrez l'opérateur Trier disparaître. SQL Server a décidé dans l'ensemble, l'utilisation du parallélisme ici a été préférée, bien qu'elle entraîne l'ajout d'un tri explicite. Mais encore une fois, cette partie du plan représente une petite partie du travail dans le grand schéma des choses.
De même, l'entrée interne de la jointure Nested Loops commence par calculer les intervalles d'approvisionnement. Curieusement, SQL Server a choisi d'utiliser des opérateurs en mode ligne pour gérer cette partie. D'une part, les opérateurs en mode ligne utilisés pour calculer les totaux cumulés impliquent plus de surcharge que l'alternative Window Aggregate en mode batch; d'autre part, SQL Server a une implémentation parallèle efficace d'une opération d'index préservant l'ordre suivie du calcul de la fonction de fenêtre, évitant un tri explicite pour cette partie. Il est curieux que l'optimiseur ait choisi une stratégie pour les intervalles de demande et une autre pour les intervalles d'approvisionnement. Dans tous les cas, l'opérateur Index Seek récupère les entrées d'approvisionnement et la séquence d'opérateurs suivante jusqu'à l'opérateur Compute Scalar calcule le délimiteur de fin d'intervalle d'approvisionnement (appelé Expr1009 dans ce plan). Le délimiteur de début d'intervalle d'approvisionnement est alors Expr1009 - Quantité (à partir de S).
Malgré la quantité de texte que j'ai utilisé pour décrire ces deux parties, la partie la plus coûteuse du travail dans le plan est ce qui vient ensuite.
La partie suivante doit joindre les intervalles de demande et les intervalles d'approvisionnement en utilisant le prédicat suivant :
D.StartDemandS.StartSupply En l'absence d'index de prise en charge, en supposant des intervalles de demande DI et des intervalles d'approvisionnement SI, cela impliquerait le traitement des lignes DI * SI. Le plan de la figure 2 a été créé après avoir rempli la table Auctions avec 400 000 lignes (200 000 entrées de demande et 200 000 entrées d'approvisionnement). Ainsi, sans index de prise en charge, le plan aurait dû traiter 200 000 * 200 000 =40 000 000 000 lignes. Pour atténuer ce coût, l'optimiseur a choisi de créer un index temporaire (voir l'opérateur Index Spool) avec le délimiteur de fin d'intervalle d'approvisionnement (Expr1009) comme clé. C'est à peu près le mieux qu'il puisse faire. Cependant, cela ne résout qu'une partie du problème. Avec deux prédicats de plage, un seul peut être pris en charge par un prédicat de recherche d'index. L'autre doit être manipulé à l'aide d'un prédicat résiduel. En effet, vous pouvez voir dans le plan que la recherche dans l'index temporaire utilise le prédicat de recherche Expr1009> Expr1005 – D.Quantity, suivi d'un opérateur Filter gérant le prédicat résiduel Expr1005> Expr1009 – S.Quantity.
En supposant qu'en moyenne, le prédicat de recherche isole la moitié des lignes d'approvisionnement de l'index par ligne de demande, le nombre total de lignes émises par l'opérateur Index Spool et traitées par l'opérateur Filter est alors DI * SI / 2. Dans notre cas, avec 200 000 lignes de demande et 200 000 lignes d'approvisionnement, cela se traduit par 20 000 000 000. En effet, la flèche allant de l'opérateur Index Spool à l'opérateur Filtre rapporte un nombre de lignes proche de celui-ci.
Ce plan a une mise à l'échelle quadratique, par rapport à la mise à l'échelle linéaire de la solution basée sur le curseur du mois dernier. Vous pouvez voir le résultat d'un test de performance comparant les deux solutions dans la figure 3. Vous pouvez clairement voir la parabole bien formée pour la solution basée sur un ensemble.
Figure 3 :Performances des intersections à l'aide de la solution CTE par rapport à la solution basée sur le curseur
Intersections d'intervalle à l'aide de tables temporaires
Vous pouvez quelque peu améliorer les choses en remplaçant l'utilisation des CTE pour les intervalles de demande et d'approvisionnement par des tables temporaires, et pour éviter la bobine d'index, en créant votre propre index sur la table temporaire contenant les intervalles d'approvisionnement avec le délimiteur de fin comme clé. Voici le code complet de la solution :
-- Supprimer les tables temporaires si elles existent.DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply ; WITH D0 AS-- D0 calcule la demande en cours comme EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extraits prev EndDemand as StartDemand, exprimant la demande début-fin sous la forme d'un intervalleD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0)SELECT ID, Quantity, CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand, CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemandINTO #DemandFROM D;WITH S0 AS-- S0 calcule l'approvisionnement en cours comme EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S extrait prev EndSupply as StartSupply, exprimant l'approvisionnement début-fin sous forme d'intervalleS AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)SELECT ID, Quantité, CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply, CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupplyINTO #SupplyFROM S ; CRÉER UN INDEX EN GROUPE UNIQUE idx_cl_ES_ID ON #Supply(EndSupply, ID); -- La requête externe identifie les échanges comme les segments qui se chevauchent des intervalles qui se croisent -- Dans les intervalles de demande et d'approvisionnement qui se croisent, la quantité de commerce est alors -- LEAST(EndDemand, EndSupply) - GREATEST(StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID AS SupplyID, CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply END AS TradeQuantityINTO #MyPairingsFROM #Demand AS D INNER JOIN #Supply AS S WITH (FORCESEEK) ON D.StartDemand S.StartSupply ; Les plans de cette solution sont illustrés à la figure 4 :
Figure 4 :Plan de requête pour les intersections à l'aide de la solution de tables temporaires
Les deux premiers plans utilisent une combinaison d'opérateurs Index Seek + Sort + Window Aggregate en mode batch pour calculer les intervalles d'offre et de demande et les écrire dans des tables temporaires. Le troisième plan gère la création d'index sur la table #Supply avec le délimiteur EndSupply comme clé principale.
Le quatrième plan représente de loin l'essentiel du travail, avec un opérateur de jointure Nested Loops qui correspond à chaque intervalle de #Demand, les intervalles d'intersection de #Supply. Notez qu'ici également, l'opérateur Index Seek s'appuie sur le prédicat #Supply.EndSupply> #Demand.StartDemand comme prédicat de recherche, et #Demand.EndDemand> #Supply.StartSupply comme prédicat résiduel. Ainsi, en termes de complexité/mise à l'échelle, vous obtenez la même complexité quadratique que pour la solution précédente. Vous payez simplement moins par ligne puisque vous utilisez votre propre index au lieu de la bobine d'index utilisée par le plan précédent. Vous pouvez voir les performances de cette solution par rapport aux deux précédentes dans la figure 5.
Figure 5 :performances des intersections à l'aide de tables temporaires par rapport aux deux autres solutions
Comme vous pouvez le voir, la solution avec les tables temporaires fonctionne mieux que celle avec les CTE, mais elle a toujours une mise à l'échelle quadratique et se comporte très mal par rapport au curseur.
Quelle est la prochaine ?
Cet article a couvert la première tentative de gestion de la tâche classique de mise en correspondance de l'offre et de la demande à l'aide d'une solution basée sur un ensemble. L'idée était de modéliser les données sous forme d'intervalles, de faire correspondre l'offre avec les entrées de demande en identifiant les intervalles d'offre et de demande qui se croisent, puis de calculer la quantité d'échanges en fonction de la taille des segments qui se chevauchent. Certainement une idée intrigante. Le problème principal avec cela est aussi le problème classique d'identification de l'intersection d'intervalle en utilisant deux prédicats de plage. Même avec le meilleur index en place, vous ne pouvez prendre en charge qu'un seul prédicat de plage avec une recherche d'index; l'autre prédicat de plage doit être géré à l'aide d'un prédicat résiduel. Il en résulte un plan avec une complexité quadratique.
Alors que pouvez-vous faire pour surmonter cet obstacle ? Il y a plusieurs idées différentes. Une idée brillante appartient à Joe Obbish, que vous pouvez lire en détail dans son article de blog. Je couvrirai d'autres idées dans les prochains articles de la série.
[ Sauter vers :défi original | solutions :partie 1 | Partie 2 | Partie 3 ]
