Estimation de jointure SQL Server à l'aide de l'alignement grossier d'histogramme

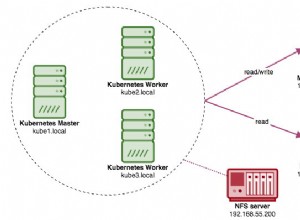
Les principales modifications apportées à l'estimation de la cardinalité à partir de la version SQL Server 2014 sont décrites dans le livre blanc Microsoft Optimisation de vos plans de requête avec l'estimateur de cardinalité SQL Server 2014 par Joe Sack, Yi Fang et Vassilis Papadimos.

L'un de ces changements concerne l'estimation des jointures simples avec un seul prédicat d'égalité ou d'inégalité à l'aide d'histogrammes statistiques. Dans la section intitulée "Join Estimate Algorithm Changes", l'article a introduit le concept d'"alignement grossier" en utilisant les limites minimales et maximales de l'histogramme :

Bien que potentiellement moins cohérent, l'ancien CE peut produire des estimations de condition de jointure simple légèrement meilleures en raison de l'alignement pas à pas de l'histogramme. Le nouveau CE utilise un alignement grossier. Cependant, la différence entre les estimations peut être suffisamment faible pour qu'elle soit moins susceptible d'entraîner un problème de qualité du plan.

En tant que l'un des réviseurs techniques de l'article, j'ai pensé qu'un peu plus de détails sur ce changement auraient été utiles, mais cela n'a pas été intégré à la version finale. Cet article ajoute certains de ces détails.

Exemple d'alignement d'histogramme grossier

L'alignement grossier L'exemple du livre blanc utilise la version Data Warehouse de l'exemple de base de données AdventureWorks. Malgré son nom, la base de données est plutôt petite; la sauvegarde ne fait que 22,3 Mo et s'étend à environ 200 Mo. Il peut être téléchargé via des liens sur la page de documentation d'installation et de configuration d'AdventureWorks.

La requête qui nous intéresse rejoint le FactResellerSales et FactCurrencyRate tableaux.

SELECT
    FRS.ProductKey,
    FRS.OrderDateKey,
    FRS.DueDateKey,
    FRS.ShipDateKey,
    FCR.DateKey,
    FCR.AverageRate,
    FCR.EndOfDayRate,
    FCR.[Date]
FROM dbo.FactResellerSales AS FRS
JOIN dbo.FactCurrencyRate AS FCR
    ON FCR.CurrencyKey = FRS.CurrencyKey;

Il s'agit d'une équijointure simple sur une seule colonne il se qualifie donc pour la cardinalité de jointure et l'estimation de la sélectivité à l'aide de l'alignement grossier de l'histogramme.

Histogrammes

Les histogrammes dont nous avons besoin sont associés au CurrencyKey colonne sur chaque table jointe. Sur une nouvelle copie de la base de données AdventureWorksDW, les statistiques préexistantes pour le plus grand FactResellerSales table sont basées sur un échantillon. Pour maximiser la reproductibilité et rendre les calculs détaillés aussi simples que possible à suivre (en évitant la mise à l'échelle), la première chose que nous allons faire est de rafraîchir les statistiques à l'aide d'un scan complet :

UPDATE STATISTICS dbo.FactCurrencyRate WITH FULLSCAN;
UPDATE STATISTICS dbo.FactResellerSales WITH FULLSCAN;

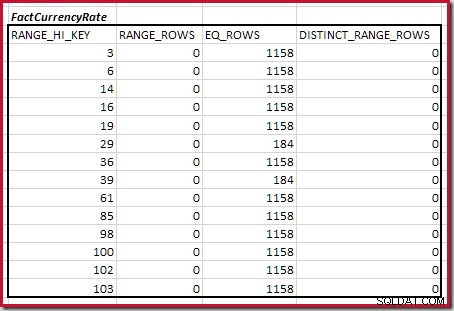
Ces tables ont l'avantage de créer des maxdiff petits et simples. histogrammes :

DBCC SHOW_STATISTICS
    (FactResellerSales, CurrencyKey)
WITH HISTOGRAM;
 
DBCC SHOW_STATISTICS
    (FactCurrencyRate, [PK_FactCurrencyRate_CurrencyKey_DateKey])
WITH HISTOGRAM;

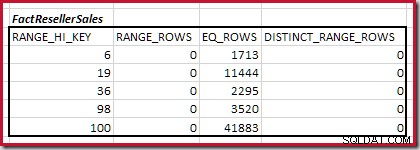
Combiner les étapes minimales d'histogramme correspondant

La première étape de l'alignement grossier Le calcul consiste à trouver la contribution à la cardinalité de jointure fournie par le pas d'histogramme correspondant le plus bas. Pour nos exemples d'histogrammes, la valeur de pas de correspondance minimale est sur RANGE_HI_KEY = 6 :

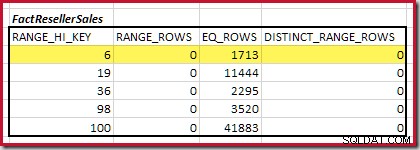
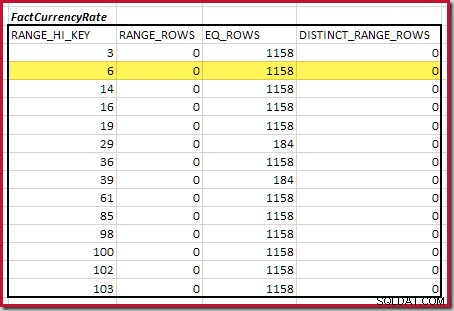
La cardinalité d'équijointure estimée pour cette étape en surbrillance est de 1 713 * 1 158 =1 983 654 lignes .

Étapes correspondantes restantes

Ensuite, nous devons identifier la plage d'histogramme RANGE_HI_KEY monte au maximum pour les correspondances d'équijointure possibles. Cela implique d'avancer à partir du minimum précédemment trouvé jusqu'à ce que l'une des entrées de l'histogramme manque de lignes. Les plages d'équijointure correspondantes pour l'exemple actuel sont mises en évidence ci-dessous :

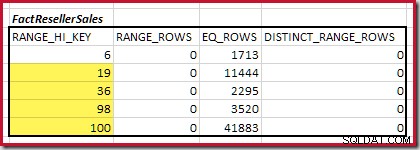
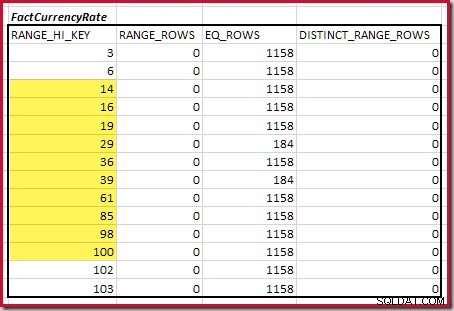
Ces deux plages représentent les lignes restantes susceptibles de contribuer à la cardinalité d'équijointure.

Estimation grossière basée sur la fréquence

La question est maintenant de savoir comment effectuer un grossier estimation de la cardinalité d'équijointure des étapes mises en évidence, à l'aide des informations disponibles.

L'estimateur de cardinalité d'origine aurait effectué un alignement d'histogramme étape par étape à grain fin en utilisant une interpolation linéaire, évalué la contribution de jointure de chaque étape (un peu comme nous l'avons fait pour la valeur d'étape minimale auparavant) et additionné chaque contribution d'étape pour acquérir un estimation complète de la jointure. Bien que cette procédure ait beaucoup de sens intuitif, l'expérience pratique a montré que cette approche fine ajoutait une surcharge de calcul et pouvait produire des résultats de qualité variable.

L'estimateur d'origine avait une autre façon d'estimer la cardinalité de jointure lorsque les informations d'histogramme n'étaient pas disponibles ou évaluées de manière heuristique comme étant inférieures. Ceci est connu sous le nom d'estimation basée sur la fréquence et utilise les définitions suivantes :

• C – la cardinalité (nombre de lignes)
• D – le nombre de valeurs distinctes
• F - la fréquence (nombre de lignes) pour chaque valeur distincte
• Remarque C =D * F par définition

L'effet d'une équijointure des relations R1 et R2 sur chacune de ces propriétés est comme indiqué ci-dessous :

• F' =F1 * F2
• D' =MIN(D1; D2) – en supposant un confinement
• C' =D' * F' (encore une fois, par définition)

Nous sommes après C', le cardinal de l'équijointure. Remplacer D' et F' dans la formule, et développer :

• C' =D' * F'
• C' =MIN(D1; D2) * F1 * F2
• C' =MIN(D1 * F1 * F2; D2 * F1 * F2)
• maintenant, puisque C1 =D1 * F1, et C2 =D2 * F2 :
• C' =MIN(C1 * F2, C2 * F1)
• enfin, puisque F =C/D (également par définition) :
• C' =MIN(C1 * C2 / D2; C2 * C1 / D1)

En notant que C1 * C2 est le produit des deux cardinalités d'entrée (jointure cartésienne), il est clair que le minimum de ces expressions sera celui avec le plus grand nombre de valeurs distinctes :

• C' =(C1 * C2) / MAX(D1 ; D2)

Dans le cas où tout cela semble un peu abstrait, une façon intuitive de penser à l'estimation d'équijointure basée sur la fréquence consiste à considérer que chaque valeur distincte d'une relation rejoindra un certain nombre de lignes (la fréquence moyenne) dans l'autre relation. Si nous avons 5 valeurs distinctes d'un côté, et que chaque valeur distincte de l'autre côté apparaît 3 fois en moyenne, une estimation d'équijointure raisonnable (mais grossière) est 5 * 3 =15.

Ce n'est pas un pinceau aussi large qu'il n'y paraît. N'oubliez pas que la cardinalité et les valeurs distinctes ci-dessus ne proviennent pas de la relation entière, mais uniquement des étapes de correspondance au-dessus du minimum. D'où une estimation grossière entre les valeurs minimales et maximales.

Calcul de fréquence

Nous pouvons obtenir chacun de ces paramètres à partir des étapes de l'histogramme en surbrillance.

• La cardinalité C est la somme de EQ_ROWS et RANGE_ROWS .
• Le nombre de valeurs distinctes D est la somme de DISTINCT_RANGE_ROWS plus un pour chaque étape.

La cardinalité C1 de la correspondance FactResellerSales étapes est la somme des cellules en surbrillance :

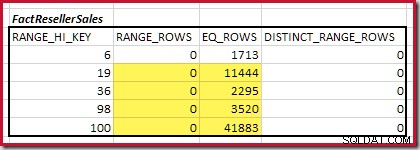
Cela donne C1 =59 142 lignes.

Il n'y a pas de lignes de plage distinctes, donc les seules valeurs distinctes proviennent des limites des quatre étapes elles-mêmes, ce qui donne D1 =4 .

Pour le second tableau :

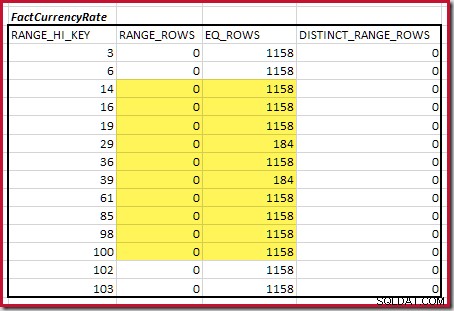
Cela donne C2 =9 632 . Encore une fois, il n'y a pas de lignes de plage distinctes, donc les valeurs distinctes proviennent des limites des dix étapes, D2 =10.

Réalisation de l'estimation Equijoin

Nous avons maintenant tous les nombres dont nous avons besoin pour la formule d'équijointure :

• C' =(C1 * C2) / MAX(D1; D2)
• C' =(59142 * 9632) / MAX(4 ; 10)
• C' =569655744 / 10
• C' =56 965 574,4

N'oubliez pas qu'il s'agit de la contribution des étapes de l'histogramme au-dessus de la limite minimale adaptée. Pour terminer l'estimation de la cardinalité de jointure, nous devons ajouter la contribution des valeurs d'étape de correspondance minimales, qui était de 1 713 * 1 158 =1 983 654 lignes.

L'estimation finale de l'équijointure est donc de 56 965 574,4 + 1 983 654 =58 949 228,4 lignes ou 58 949 200 à six chiffres significatifs.

Ce résultat est confirmé dans le plan d'exécution estimé pour la requête source :

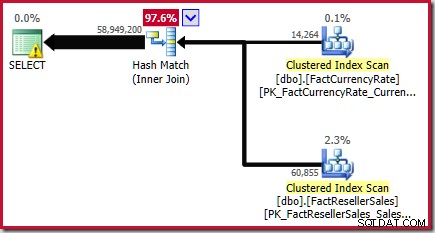
Comme indiqué dans le Livre blanc, ce n'est pas une bonne estimation. Le nombre réel de lignes renvoyées par cette requête est 70 470 090 . L'estimation produite par l'estimateur de cardinalité d'origine ("hérité") - en utilisant l'alignement d'histogramme étape par étape - est de 70 470 100 lignes.

De meilleurs résultats sont souvent possibles avec la méthode plus fine, mais seulement si les statistiques sont une très bonne représentation de la distribution sous-jacente des données. Il ne s'agit pas simplement de tenir à jour des statistiques ou d'utiliser une analyse complète de la population. L'algorithme utilisé pour regrouper les informations dans un maximum de 201 étapes d'histogramme n'est pas parfait et, dans tous les cas, de nombreuses distributions de données réelles ne sont tout simplement pas capables d'une telle fidélité d'histogramme. En moyenne, les gens devraient trouver que la méthode plus grossière fournit des estimations parfaitement adéquates et une plus grande stabilité avec le nouveau CE.

Deuxième exemple

Cela s'appuie un peu sur l'exemple précédent et ne nécessite pas de téléchargement d'un exemple de base de données.

DROP TABLE IF EXISTS
    dbo.R1,
    dbo.R2;
 
CREATE TABLE dbo.R1 (n integer NOT NULL);
CREATE TABLE dbo.R2 (n integer NOT NULL);
 
INSERT dbo.R1
    (n)
VALUES
    (1), (2), (3), (4), (5), (6), (7), (8), (9), (10),
    (6), (6), (6), (6), (6), (6), (6), (6), (6), (6), 
    (6), (6), (6), (6), (6), (6), (6), (6), (6);
 
INSERT dbo.R2
    (n)
VALUES
    (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15),
    (10), (10);
 
CREATE STATISTICS stats_n ON dbo.R1 (n) WITH FULLSCAN;
CREATE STATISTICS stats_n ON dbo.R2 (n) WITH FULLSCAN;

Les histogrammes montrant les étapes minimales correspondantes sont :

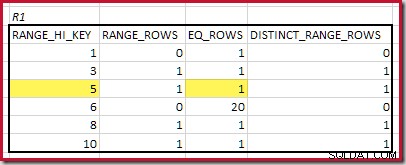
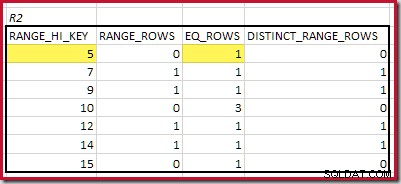
Le RANGE_HI_KEY le plus bas qui correspond est 5. La valeur de EQ_ROWS est 1 dans les deux, donc la cardinalité d'équijointure estimée est 1 * 1 =1 ligne .

Le RANGE_HI_KEY correspondant le plus élevé est 10. Mise en surbrillance des lignes de l'histogramme R1 pour une estimation grossière basée sur la fréquence :

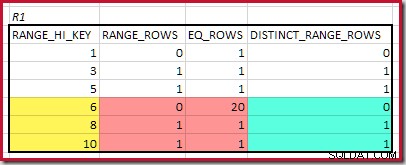
Sommation EQ_ROWS et RANGE_ROWS donne C1 =24 . Le nombre de lignes distinctes est de 2 DISTINCT_RANGE_ROWS (valeurs distinctes entre les étapes) plus 3 pour les valeurs distinctes associées à chaque limite d'étape, ce qui donne D1 =5 .

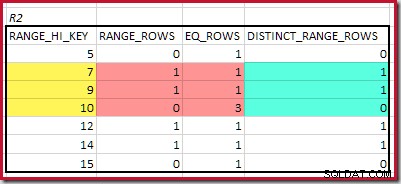
Pour R2, additionner EQ_ROWS et RANGE_ROWS donne C2 =7 . Le nombre de lignes distinctes est de 2 DISTINCT_RANGE_ROWS (valeurs distinctes entre les étapes) plus 3 pour les valeurs distinctes associées à chaque limite d'étape, ce qui donne D2 =5 .

L'estimation d'équijointure C' est :

• C' =(C1 * C2) / MAX(D1; D2)
• C' =(24 * 7) / 5
• C' =33,6

Ajout dans la 1 ligne à partir de la correspondance d'étape minimale donne une estimation totale de 34,6 lignes pour l'équijointure :

SELECT
    R1.n,
    R2.n
FROM dbo.R1 AS R1
JOIN dbo.R2 AS R2
    ON R2.n = R1.n;

Le plan d'exécution estimé affiche une estimation correspondant à notre calcul :

Ce n'est pas tout à fait exact, mais l'estimateur de cardinalité "hérité" ne fait pas mieux, estimant 15,25 lignes contre 27 réelles :

Pour un traitement complet, nous devrions également ajouter une contribution finale des étapes nulles de l'histogramme correspondant, mais cela est rare pour les équijointures (qui sont généralement écrites pour rejeter les valeurs nulles) et une extension relativement simple pour le lecteur intéressé.

Réflexions finales

Espérons que les détails de l'article combleront quelques lacunes pour tous ceux qui se sont déjà interrogés sur "l'alignement grossier". Notez qu'il ne s'agit que d'un petit composant de l'estimateur de cardinalité. Il existe plusieurs autres concepts et algorithmes importants utilisés pour l'estimation de jointure, notamment la manière dont les prédicats de non-jointure sont évalués et la manière dont les jointures plus complexes sont gérées. La plupart des éléments vraiment importants sont assez bien couverts dans le livre blanc.