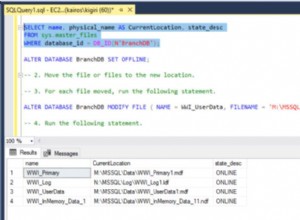
La documentation
est un peu incomplet quant à la magie de la valeur 6 et quand appliquer le max fonction, mais voici un tableau de mes conclusions, basé sur cette documentation.
Comme il est dit, les formules de division sont :
Et, comme vous le soulignez vous-même, nous avons ensuite la note de bas de page :
Alors, voici ce que j'ai produit dans ma feuille de calcul :
p1 s1 p2 s2 prInit srInit prOver prAdjusted srAdjusted
38 16 38 16 93 55 55 38 6
28 16 28 16 73 45 35 38 10
29 16 29 16 75 46 37 38 9
Donc, j'utilise pr et sr pour indiquer la précision et l'échelle du résultat. Le prInit et srInit les formules sont exactement les formules de la documentation. Comme nous pouvons le voir, dans les 3 cas, la précision du résultat est largement supérieure à 38 et donc la note de bas de page s'applique. prOver est juste max(0,prInit - 38) - de combien devons-nous ajuster la précision si la note de bas de page s'applique. prAdjusted est juste prInit - prOver . Nous pouvons voir dans les trois cas que la précision finale du résultat est 38 .
Si j'applique le même facteur d'ajustement aux échelles alors j'obtiendrais des résultats de 0 , 10 et 9 . Mais nous pouvons voir que votre résultat pour le (38,16) le cas a une échelle de 6 . Donc je crois que c'est là que le max(6,... une partie de la documentation s'applique réellement. Donc ma formule finale pour srAdjusted est max(6,srInit-prOver) et maintenant mon dernier Adjusted les valeurs semblent correspondre à vos résultats.
Et, bien sûr, si nous consultons la documentation pour decimal
, nous pouvons voir que la valeur par défaut la précision et l'échelle, si vous ne les spécifiez pas, sont (18,0) , voici donc la ligne pour laquelle vous n'avez pas spécifié la précision et l'échelle :
p1 s1 p2 s2 prInit srInit prOver prAdjusted srAdjusted
18 0 18 0 37 19 0 37 19