Une partie importante du réglage des requêtes consiste à comprendre les algorithmes dont dispose l'optimiseur pour gérer diverses constructions de requête, par exemple, le filtrage, la jointure, le regroupement et l'agrégation, et leur mise à l'échelle. Cette connaissance vous aide à préparer un environnement physique optimal pour vos requêtes, comme la création des bons index. Il vous aide également à détecter intuitivement quel algorithme vous devriez vous attendre à voir dans le plan dans un certain ensemble de circonstances, en fonction de votre familiarité avec les seuils où l'optimiseur doit passer d'un algorithme à un autre. Ensuite, lors du réglage des requêtes peu performantes, vous pouvez plus facilement repérer les zones du plan de requête où l'optimiseur peut avoir fait des choix sous-optimaux, par exemple en raison d'estimations de cardinalité inexactes, et prendre des mesures pour les corriger.
Une autre partie importante du réglage des requêtes consiste à sortir des sentiers battus - au-delà des algorithmes disponibles pour l'optimiseur lors de l'utilisation des outils évidents. Sois créatif. Supposons que vous ayez une requête qui fonctionne mal même si vous avez organisé l'environnement physique optimal. Pour les constructions de requête que vous avez utilisées, les algorithmes disponibles pour l'optimiseur sont x, y et z, et l'optimiseur a choisi du mieux qu'il pouvait dans les circonstances. Pourtant, la requête fonctionne mal. Pouvez-vous imaginer un plan théorique avec un algorithme qui peut produire une requête beaucoup plus performante ? Si vous pouvez l'imaginer, il y a de fortes chances que vous puissiez y parvenir avec une réécriture de requête, peut-être avec des constructions de requête moins évidentes pour la tâche.
Dans cette série d'articles, je me concentre sur le regroupement et l'agrégation de données. Je vais commencer par passer en revue les algorithmes disponibles pour l'optimiseur lors de l'utilisation de requêtes groupées. Je décrirai ensuite des scénarios où aucun des algorithmes existants ne fonctionne bien et montrerai des réécritures de requêtes qui se traduisent par d'excellentes performances et une mise à l'échelle.
J'aimerais remercier Craig Freedman, Vassilis Papadimos et Joe Sack, membres de l'intersection de l'ensemble des personnes les plus intelligentes de la planète et de l'ensemble des développeurs SQL Server, pour avoir répondu à mes questions sur l'optimisation des requêtes !
Pour les exemples de données, j'utiliserai une base de données appelée PerformanceV3. Vous pouvez télécharger un script pour créer et remplir la base de données à partir d'ici. Je vais utiliser une table appelée dbo.Orders, qui contient 1 000 000 de lignes. Cette table contient quelques index qui ne sont pas nécessaires et qui pourraient interférer avec mes exemples, alors exécutez le code suivant pour supprimer ces index inutiles :
DROP INDEX idx_nc_sid_od_cid ON dbo.Orders; DROP INDEX idx_unc_od_oid_i_cid_eid ON dbo.Orders;
Les deux seuls index restants sur cette table sont un index cluster appelé idx_cl_od sur la colonne orderdate et un index unique non cluster appelé PK_Orders sur la colonne orderid, appliquant la contrainte de clé primaire.
EXEC sys.sp_helpindex 'dbo.Orders';
index_name index_description index_keys ----------- ----------------------------------------------------- ----------- idx_cl_od clustered located on PRIMARY orderdate PK_Orders nonclustered, unique, primary key located on PRIMARY orderid
Algorithmes existants
SQL Server prend en charge deux algorithmes principaux pour agréger les données :Stream Aggregate et Hash Aggregate. Avec les requêtes groupées, l'algorithme Stream Aggregate nécessite que les données soient triées par les colonnes groupées, vous devez donc faire la distinction entre deux cas. L'un est un Stream Aggregate préordonné, par exemple, lorsque les données sont obtenues préordonnées à partir d'un index. Un autre est un Stream Aggregate non préordonné, où une étape supplémentaire est nécessaire pour trier explicitement l'entrée. Ces deux cas évoluent très différemment, vous pouvez donc aussi bien les considérer comme deux algorithmes différents.
L'algorithme Hash Aggregate organise les groupes et leurs agrégats dans une table de hachage. Il ne nécessite pas l'entrée pour être commandé.
Avec suffisamment de données, l'optimiseur envisage de paralléliser le travail, en appliquant ce qu'on appelle un agrégat local-global. Dans un tel cas, l'entrée est divisée en plusieurs threads, et chaque thread applique l'un des algorithmes susmentionnés pour agréger localement son sous-ensemble de lignes. Un agrégat global utilise ensuite l'un des algorithmes susmentionnés pour agréger les résultats des agrégats locaux.
Dans cet article, je me concentre sur l'algorithme Stream Aggregate préordonné et sa mise à l'échelle. Dans les prochaines parties de cette série, je couvrirai d'autres algorithmes et décrirai les seuils où l'optimiseur passe de l'un à l'autre, et quand vous devriez envisager des réécritures de requête.
Agrégat de flux précommandé
Étant donné une requête groupée avec un ensemble de regroupement non vide (l'ensemble d'expressions par lequel vous regroupez), l'algorithme Stream Aggregate nécessite que les lignes d'entrée soient triées par les expressions formant l'ensemble de regroupement. Lorsque l'algorithme traite la première ligne d'un groupe, il initialise un membre contenant la valeur d'agrégat intermédiaire avec la valeur pertinente (par exemple, la valeur de la première ligne pour un agrégat MAX). Lorsqu'il traite une autre ligne du groupe, il attribue à ce membre le résultat d'un calcul impliquant la valeur d'agrégat intermédiaire et la valeur de la nouvelle ligne (par exemple, le maximum entre la valeur d'agrégat intermédiaire et la nouvelle valeur). Dès que l'un des membres du groupement change de valeur ou que l'entrée est consommée, la valeur agrégée actuelle est considérée comme le résultat final pour le dernier groupe.
Une façon d'avoir les données ordonnées comme l'algorithme Stream Aggregate en a besoin est de les obtenir préordonnées à partir d'un index. Vous avez besoin que l'index soit défini avec les colonnes du jeu de regroupement comme clés, dans n'importe quel ordre parmi elles. Vous voulez également que l'index soit couvrant. Par exemple, considérez la requête suivante (nous l'appellerons Requête 1) :
SELECT shipperid, MAX(orderdate) AS maxorderid FROM dbo.Orders GROUP BY shipperid;
Un index rowstore optimal pour prendre en charge cette requête serait un index défini avec shipperid comme colonne clé principale et date de commande soit comme colonne incluse, soit comme deuxième colonne clé :
CREATE INDEX idx_sid_od ON dbo.Orders(shipperid, orderdate);
Avec cet index en place, vous obtenez le plan estimé illustré à la figure 1 (à l'aide de SentryOne Plan Explorer).

Figure 1 :Plan pour la requête 1
Notez que l'opérateur Index Scan a une propriété Ordered:True signifiant qu'il est nécessaire de livrer les lignes ordonnées par la clé d'index. L'opérateur Stream Aggregate ingère ensuite les lignes ordonnées selon ses besoins. Quant à la façon dont le coût de l'opérateur est calculé ; avant d'en arriver là, une petite préface d'abord…
Comme vous le savez peut-être déjà, lorsque SQL Server optimise une requête, il évalue plusieurs plans candidats et choisit finalement celui dont le coût estimé est le plus bas. Le coût estimé du plan est la somme de tous les coûts estimés des opérateurs. À son tour, le coût estimé de chaque opérateur est la somme du coût d'E/S estimé et du coût CPU estimé. L'unité de coût n'a pas de sens en soi. Sa pertinence réside dans la comparaison que l'optimiseur effectue entre les plans candidats. Autrement dit, les formules d'établissement des coûts ont été conçues dans le but que, entre les plans candidats, celui dont le coût est le plus bas représente (espérons-le) celui qui se terminera le plus rapidement. Une tâche terriblement complexe à faire avec précision !
Plus les formules de calcul des coûts prennent en compte de manière adéquate les facteurs qui affectent réellement les performances et la mise à l'échelle de l'algorithme, plus elles sont précises et plus il est probable que, compte tenu des estimations de cardinalité précises, l'optimiseur choisira le plan optimal. Quoi qu'il en soit, si vous voulez comprendre pourquoi l'optimiseur choisit un algorithme plutôt qu'un autre, vous devez comprendre deux éléments principaux :l'un est le fonctionnement et l'échelle des algorithmes, et l'autre est le modèle d'établissement des coûts de SQL Server.
Revenons donc au plan de la figure 1 ; essayons de comprendre comment les coûts sont calculés. En tant que politique, Microsoft ne révélera pas les formules de coûts internes qu'ils utilisent. Quand j'étais enfant, j'étais fasciné par le démontage. Montres, radios, cassettes (oui, je suis si vieux), etc. Je voulais savoir comment les choses étaient faites. De même, je vois de l'intérêt dans l'ingénierie inverse des formules car si je parviens à prédire le coût avec une précision raisonnable, cela signifie probablement que je comprends bien l'algorithme. Au cours du processus, vous apprendrez beaucoup.
Notre requête ingère 1 000 000 lignes. Même avec ce nombre de lignes, le coût des E/S semble être négligeable par rapport au coût du processeur, il est donc probablement prudent de l'ignorer.
En ce qui concerne le coût du processeur, vous voulez essayer de déterminer quels facteurs l'affectent et de quelle manière. Théoriquement, il pourrait y avoir un certain nombre de facteurs :nombre de lignes d'entrée, nombre de groupes, cardinalité de l'ensemble de regroupement, type de données et taille des membres de l'ensemble de regroupement. Ainsi, pour essayer de mesurer l'effet de l'un de ces facteurs, vous souhaitez comparer les coûts estimés de deux requêtes qui ne diffèrent que par le facteur que vous souhaitez mesurer. Par exemple, pour mesurer l'impact du nombre de lignes sur le coût, ayez deux requêtes avec un nombre différent de lignes d'entrée, mais avec tous les autres aspects identiques (nombre de groupes, cardinalité de l'ensemble de regroupement, etc.). En outre, il est important de vérifier que les chiffres estimés (et non les chiffres réels) sont ceux souhaités, car l'optimiseur s'appuie sur les chiffres estimés pour calculer les coûts.
Lorsque vous faites de telles comparaisons, il est bon d'avoir des techniques qui vous permettent de contrôler entièrement les nombres estimés. Par exemple, un moyen simple de contrôler le nombre estimé de lignes d'entrée consiste à interroger une expression de table basée sur une requête TOP et à appliquer la fonction d'agrégation dans la requête externe. Si vous craignez qu'en raison de votre utilisation de l'opérateur TOP, l'optimiseur applique des objectifs de ligne et que ceux-ci entraînent un ajustement des coûts d'origine, cela ne s'applique qu'aux opérateurs qui apparaissent dans le plan sous l'opérateur Top (au droite), pas au-dessus (vers la gauche). L'opérateur Stream Aggregate apparaît naturellement au-dessus de l'opérateur Top dans le plan puisqu'il ingère les lignes filtrées.
En ce qui concerne le contrôle du nombre estimé de groupes de sortie, vous pouvez le faire en utilisant l'expression de regroupement
Pour vous assurer que vous obtenez l'algorithme Stream Aggregate et un plan série, vous pouvez le forcer avec les indicateurs de requête :OPTION(ORDER GROUP, MAXDOP 1).
Vous voulez également déterminer s'il y a un coût de démarrage pour l'opérateur afin de pouvoir en tenir compte dans votre formule de rétro-ingénierie.
Commençons par déterminer comment le nombre de lignes d'entrée affecte le coût CPU estimé de l'opérateur. De toute évidence, ce facteur devrait être pertinent pour le coût de l'opérateur. En outre, vous vous attendez à ce que le coût par ligne soit constant. Voici quelques requêtes de comparaison qui ne diffèrent que par le nombre estimé de lignes d'entrée (appelez-les respectivement Requête 2 et Requête 3) :
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1); SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (200000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1);
La figure 2 présente les parties pertinentes des plans estimés pour ces requêtes :

Figure 2 :Plans pour les requêtes 2 et 3
En supposant que le coût par ligne est constant, vous pouvez le calculer comme la différence entre les coûts de l'opérateur divisé par la différence entre les cardinalités d'entrée de l'opérateur :
CPU cost per row = (0.125 - 0.065) / (200000 - 100000) = 0.0000006
Pour vérifier que le nombre que vous avez obtenu est bien constant et correct, vous pouvez essayer de prédire les coûts estimés dans les requêtes avec d'autres nombres de lignes d'entrée. Par exemple, le coût prévu avec 500 000 lignes d'entrée est :
Cost for 500K input rows = <cost for 100K input rows> + 400000 * 0.0000006 = 0.065 + 0.24 = 0.305
Utilisez la requête suivante pour vérifier si votre prédiction est exacte (appelez-la Requête 4) :
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (500000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1);
La partie pertinente du plan pour cette requête est illustrée à la figure 3.
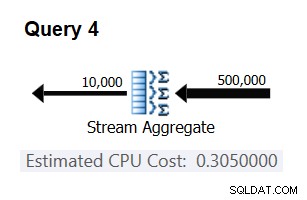
Figure 3 :Plan pour la requête 4
Bingo. Naturellement, c'est une bonne idée de vérifier plusieurs cardinalités d'entrée supplémentaires. Avec tous ceux que j'ai vérifiés, la thèse selon laquelle il y a un coût constant par ligne d'entrée de 0,0000006 était correcte.
Ensuite, essayons de comprendre comment le nombre estimé de groupes affecte le coût CPU de l'opérateur. Vous vous attendez à ce qu'un certain travail CPU soit nécessaire pour traiter chaque groupe, et il est également raisonnable de s'attendre à ce qu'il soit constant par groupe. Pour tester cette thèse et calculer le coût par groupe, vous pouvez utiliser les deux requêtes suivantes, qui ne diffèrent que par le nombre de groupes de résultats (appelez-les respectivement Requête 5 et Requête 6) :
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1); SELECT orderid % 20000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 20000 OPTION(ORDER GROUP, MAXDOP 1);
Les parties pertinentes des plans de requête estimés sont illustrées à la figure 4.
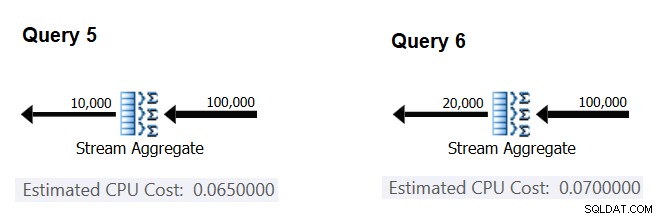
Figure 4 :Plans pour la requête 5 et la requête 6
De la même manière que vous avez calculé le coût fixe par ligne d'entrée, vous pouvez calculer le coût fixe par groupe de sortie comme la différence entre les coûts de l'opérateur divisé par la différence entre les cardinalités de sortie de l'opérateur :
CPU cost per group = (0.07 - 0.065) / (20000 - 10000) = 0.0000005
Et tout comme je l'ai démontré précédemment, vous pouvez vérifier vos résultats en prédisant les coûts avec d'autres nombres de groupes de sortie et en comparant vos nombres prédits avec ceux produits par l'optimiseur. Avec tous les nombres de groupes que j'ai essayés, les coûts prévus étaient exacts.
En utilisant des techniques similaires, vous pouvez vérifier si d'autres facteurs affectent le coût de l'opérateur. Mes tests montrent que la cardinalité de l'ensemble de regroupement (nombre d'expressions par lesquelles vous regroupez), les types de données et les tailles des expressions groupées n'ont aucun impact sur le coût estimé.
Il ne reste plus qu'à vérifier s'il y a un coût de démarrage significatif supposé pour l'opérateur. S'il y en a une, la formule complète (espérons-le) pour calculer le coût CPU de l'opérateur devrait être :
Operator CPU cost = <startup cost> + <#input rows> * 0.0000006 + <#output groups> * 0.0000005
Vous pouvez donc déduire le coût de démarrage du reste :
Startup cost =- (<#input rows> * 0.0000006 + <#output groups> * 0.0000005)
Vous pouvez utiliser n'importe quel plan de requête de cet article à cette fin. Par exemple, en utilisant les nombres du plan pour la requête 5 illustrée précédemment dans la figure 4, vous obtenez :
Startup cost = 0.065 - (100000 * 0.0000006 + 10000 * 0.0000005) = 0
Comme il semblerait, l'opérateur Stream Aggregate n'a pas de coût de démarrage lié au processeur, ou il est si faible qu'il n'est pas affiché avec la précision de la mesure du coût.
En conclusion, la formule de rétro-ingénierie pour le coût de l'opérateur Stream Aggregate est :
I/O cost: negligible CPU cost: <#input rows> * 0.0000006 + <#output groups> * 0.0000005
La figure 5 illustre la mise à l'échelle du coût de l'opérateur Stream Aggregate par rapport au nombre de lignes et au nombre de groupes.
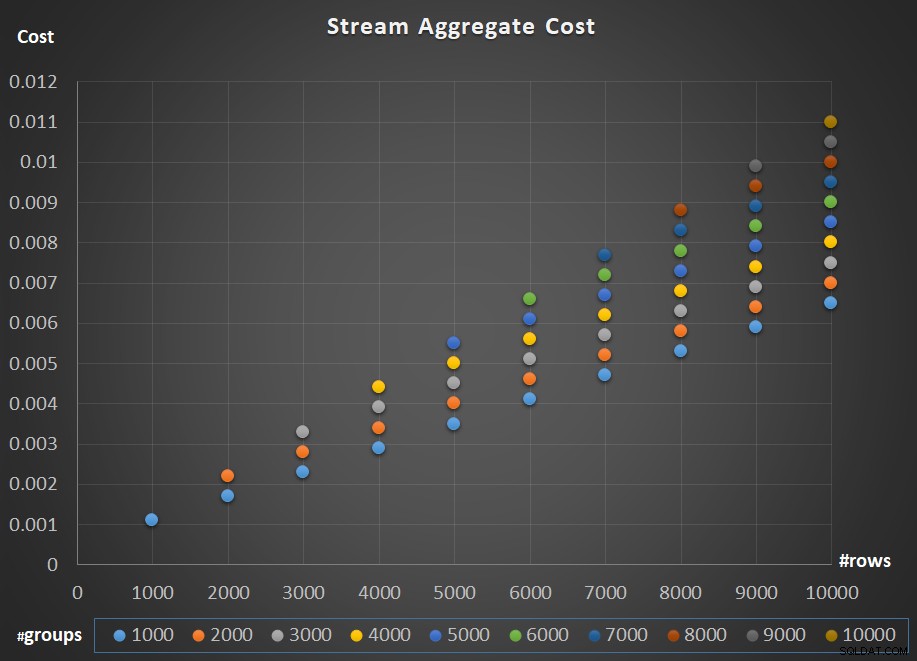
Figure 5 :Tableau de mise à l'échelle de l'algorithme Stream Aggregate
Quant à la mise à l'échelle de l'opérateur ; c'est linéaire. Dans les cas où le nombre de groupes a tendance à être proportionnel au nombre de rangées, le coût total de l'opérateur augmente du même facteur que le nombre de rangées et de groupes. Cela signifie que doubler le nombre de lignes d'entrée et de groupes d'entrée entraîne le doublement du coût total de l'opérateur. Pour comprendre pourquoi, supposons que nous représentions le coût de l'opérateur comme :
r * 0.0000006 + g * 0.0000005
Si vous augmentez à la fois le nombre de lignes et le nombre de groupes du même facteur p, vous obtenez :
pr * 0.0000006 + pg * 0.0000005 = p * (r * 0.0000006 + g * 0.0000005)
Ainsi, si, pour un nombre donné de lignes et de groupes, le coût de l'opérateur Stream Aggregate est C, augmenter à la fois le nombre de lignes et de groupes du même facteur p donne un coût d'opérateur de pC. Voyez si vous pouvez le vérifier en identifiant des exemples dans le tableau de la figure 5.
Dans les cas où le nombre de groupes reste assez stable même lorsque le nombre de lignes d'entrée augmente, vous obtenez toujours une mise à l'échelle linéaire. Considérez simplement le coût associé au nombre de groupes comme une constante. Autrement dit, si pour un nombre donné de lignes et de groupes, le coût de l'opérateur est C =G (coût associé au nombre de groupes) plus R (coût associé au nombre de lignes), en augmentant simplement le nombre de lignes d'un facteur de p donne G + pR. Dans un tel cas, naturellement, le coût total de l'opérateur est inférieur à pC. Autrement dit, doubler le nombre de rangées entraîne moins que le double du coût total de l'opérateur.
En pratique, dans de nombreux cas, lorsque vous regroupez des données, le nombre de lignes d'entrée est nettement supérieur au nombre de groupes de sortie. Ce fait, combiné au fait que le coût alloué par rang et le coût par groupe sont presque les mêmes, la part du coût de l'opérateur qui est attribuée au nombre de groupes devient négligeable. À titre d'exemple, reportez-vous au plan de la requête 1 présenté précédemment dans la figure 1. Dans de tels cas, il est prudent de considérer simplement le coût de l'opérateur comme une simple mise à l'échelle linéaire par rapport au nombre de lignes d'entrée.
Cas particuliers
Il existe des cas particuliers où l'opérateur Stream Aggregate n'a pas du tout besoin de trier les données. Si vous y réfléchissez, l'algorithme Stream Aggregate a une exigence de commande plus souple à partir de l'entrée par rapport au moment où vous avez besoin des données commandées à des fins de présentation, par exemple, lorsque la requête a une clause ORDER BY de présentation externe. L'algorithme Stream Aggregate a simplement besoin que toutes les lignes du même groupe soient triées ensemble. Prenez l'ensemble d'entrée {5, 1, 5, 2, 1, 2}. À des fins d'ordre de présentation, cet ensemble doit être ordonné comme suit :1, 1, 2, 2, 5, 5. À des fins d'agrégation, l'algorithme Stream Aggregate fonctionnerait toujours bien si les données étaient organisées dans l'ordre suivant :5, 5, 1, 1, 2, 2. Dans cet esprit, lorsque vous calculez un agrégat scalaire (requête avec une fonction d'agrégation et sans clause GROUP BY), ou regroupez les données par un ensemble de regroupement vide, il n'y a jamais plus d'un groupe . Indépendamment de l'ordre des lignes d'entrée, l'algorithme Stream Aggregate peut être appliqué. L'algorithme Hash Aggregate hache les données en fonction des expressions de l'ensemble de regroupement en tant qu'entrées, et à la fois avec des agrégats scalaires et avec un ensemble de regroupement vide, il n'y a pas d'entrées à hacher. Ainsi, à la fois avec des agrégats scalaires et avec des agrégats appliqués à un ensemble de regroupement vide, l'optimiseur utilise toujours l'algorithme Stream Aggregate, sans exiger que les données soient préordonnées. C'est au moins le cas en mode d'exécution de ligne, car actuellement (à partir de SQL Server 2017 CU4) le mode batch n'est disponible qu'avec l'algorithme Hash Aggregate. Je vais utiliser les deux requêtes suivantes pour le démontrer (appelez-les requête 7 et requête 8) :
SELECT COUNT(*) AS numrows FROM dbo.Orders; SELECT COUNT(*) AS numrows FROM dbo.Orders GROUP BY ();
Les plans de ces requêtes sont illustrés à la figure 6.
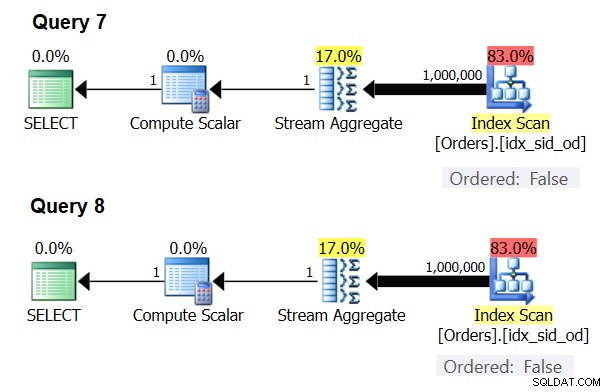
Figure 6 :Plans pour les requêtes 7 et 8
Essayez de forcer un algorithme Hash Aggregate dans les deux cas :
SELECT COUNT(*) AS numrows FROM dbo.Orders OPTION(HASH GROUP); SELECT COUNT(*) AS numrows FROM dbo.Orders GROUP BY () OPTION(HASH GROUP);
L'optimiseur ignore votre demande et produit les mêmes plans que ceux illustrés à la figure 6.
Quiz rapide :quelle est la différence entre un agrégat scalaire et un agrégat appliqué à un ensemble de regroupement vide ?
Réponse :avec un ensemble d'entrée vide, un agrégat scalaire renvoie un résultat avec une ligne, alors qu'un agrégat dans une requête avec un ensemble de regroupement vide renvoie un ensemble de résultats vide. Essayez-le :
SELECT COUNT(*) AS numrows FROM dbo.Orders WHERE 1 = 2;
numrows ----------- 0 (1 row affected)
SELECT COUNT(*) AS numrows FROM dbo.Orders WHERE 1 = 2 GROUP BY ();
numrows ----------- (0 rows affected)
Lorsque vous avez terminé, exécutez le code suivant pour le nettoyage :
DROP INDEX idx_sid_od ON dbo.Orders;
Résumé et défi
La rétro-ingénierie de la formule de calcul des coûts pour l'algorithme Stream Aggregate est un jeu d'enfant. J'aurais pu simplement vous dire que la formule de coût pour un algorithme Stream Aggregate pré-ordonné est @numrows * 0,0000006 + @numgroups * 0,0000005 au lieu d'un article entier pour expliquer comment vous comprenez cela. Il s'agissait cependant de décrire le processus et les principes de la rétro-ingénierie, avant de passer aux algorithmes plus complexes et aux seuils où un algorithme devient plus optimal que les autres. Vous apprendre à pêcher au lieu de vous donner du poisson. J'ai tellement appris et découvert des choses auxquelles je n'avais même pas pensé, tout en essayant de procéder à la rétro-ingénierie des formules de calcul des coûts pour divers algorithmes.
Prêt à tester vos compétences ? Votre mission, si vous choisissez de l'accepter, est un cran plus difficile que la rétro-ingénierie de l'opérateur Stream Aggregate. Inversez la formule de calcul des coûts d'un opérateur de tri en série. Ceci est important pour notre recherche car un algorithme Stream Aggregate appliqué à une requête avec un ensemble de regroupement non vide, où les données d'entrée ne sont pas préordonnées, nécessite un tri explicite. Dans ce cas, le coût et la mise à l'échelle de l'opération d'agrégation dépendent du coût et de la mise à l'échelle des opérateurs Sort et Stream Aggregate combinés.
Si vous parvenez à vous rapprocher décemment de la prévision du coût de l'opérateur de tri, vous pouvez avoir l'impression d'avoir gagné le droit d'ajouter à votre signature "l'ingénierie inverse". Il existe de nombreux ingénieurs en logiciel; mais vous ne voyez certainement pas beaucoup d'ingénieurs inverses ! Assurez-vous simplement de tester votre formule à la fois avec de petits nombres et avec de grands nombres; vous pourriez être surpris par ce que vous trouverez.