Renvoyer des combinaisons
À l'aide d'une table de nombres ou d'un CTE générant des nombres, sélectionnez 0 à 2 ^ n - 1. En utilisant les positions de bit contenant des 1 dans ces nombres pour indiquer la présence ou l'absence des membres relatifs dans la combinaison, et en éliminant ceux qui n'ont pas le nombre correct de valeurs, vous devriez être en mesure de renvoyer un ensemble de résultats avec toutes les combinaisons souhaitées.
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
Cette requête fonctionne plutôt bien, mais j'ai pensé à un moyen de l'optimiser, en m'inspirant du Nifty Parallel Bit Count pour obtenir d'abord le bon nombre d'éléments pris à la fois. Cela fonctionne 3 à 3,5 fois plus vite (à la fois CPU et temps):
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
Je suis allé lire la page de comptage de bits et je pense que cela pourrait mieux fonctionner si je ne fais pas le% 255 mais que je vais jusqu'au bout avec l'arithmétique des bits. Dès que j'en aurai l'occasion, j'essaierai et je verrai ce que ça donne.
Mes revendications de performances sont basées sur les requêtes exécutées sans la clause ORDER BY. Pour plus de clarté, ce que fait ce code compte le nombre de bits 1 définis dans Num à partir des Numbers table. C'est parce que le nombre est utilisé comme une sorte d'indexeur pour choisir quels éléments de l'ensemble sont dans la combinaison actuelle, donc le nombre de 1-bits sera le même.
J'espère que ça vous plaira !
Pour mémoire, cette technique d'utilisation du modèle binaire des nombres entiers pour sélectionner les membres d'un ensemble est ce que j'ai inventé le "Vertical Cross Join". Il en résulte effectivement la jointure croisée de plusieurs ensembles de données, où le nombre d'ensembles et de jointures croisées est arbitraire. Ici, le nombre d'ensembles est le nombre d'éléments pris à la fois.
En fait, la jointure croisée dans le sens horizontal habituel (d'ajouter plus de colonnes à la liste existante de colonnes avec chaque jointure) ressemblerait à ceci :
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
Mes requêtes ci-dessus "rejoignent" efficacement autant de fois que nécessaire avec une seule jointure. Les résultats ne sont pas pivotés par rapport aux jointures croisées réelles, bien sûr, mais c'est un problème mineur.
Critique de votre code
Tout d'abord, puis-je suggérer ce changement à votre FDU factoriel :
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
Maintenant, vous pouvez calculer des ensembles de combinaisons beaucoup plus grands, et c'est plus efficace. Vous pourriez même envisager d'utiliser decimal(38, 0) pour permettre des calculs intermédiaires plus importants dans vos calculs combinés.
Deuxièmement, votre requête donnée ne renvoie pas les résultats corrects. Par exemple, en utilisant mes données de test des tests de performances ci-dessous, l'ensemble 1 est identique à l'ensemble 18. Il semble que votre requête prend une bande coulissante qui s'enroule autour :chaque ensemble est toujours composé de 5 membres adjacents, ressemblant à ceci (j'ai pivoté pour le rendre plus facile à voir):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
Comparez le modèle de mes requêtes :
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
Juste pour conduire le bit-pattern -> index de combinaison à la maison pour toute personne intéressée, notez que 31 en binaire =11111 et le pattern est ABCDE. 121 en binaire est 1111001 et le modèle est A__DEFG (mappé en arrière).
Résultats de performance avec un tableau de nombres réels
J'ai effectué des tests de performances avec de grands ensembles sur ma deuxième requête ci-dessus. Je n'ai pas de trace pour le moment de la version du serveur utilisée. Voici mes données de test :
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
Peter a montré que cette "jointure croisée verticale" ne fonctionne pas aussi bien que la simple écriture de SQL dynamique pour effectuer les CROSS JOINs qu'elle évite. Au prix insignifiant de quelques lectures supplémentaires, sa solution a des métriques entre 10 et 17 fois meilleures. Les performances de sa requête diminuent plus vite que la mienne à mesure que la quantité de travail augmente, mais pas assez vite pour empêcher quiconque de l'utiliser.
La deuxième série de nombres ci-dessous est le facteur divisé par la première ligne du tableau, juste pour montrer comment il évolue.
Érik
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
Pierre
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
En extrapolant, ma requête finira par être moins chère (bien qu'elle soit dès le départ en lecture), mais pas pour longtemps. Pour utiliser 21 éléments dans l'ensemble, il faut déjà une table de nombres allant jusqu'à 2097152...
Voici un commentaire que j'ai fait à l'origine avant de réaliser que ma solution fonctionnerait considérablement mieux avec une table de nombres à la volée :
Résultats de performance avec un tableau de nombres à la volée
Lorsque j'ai initialement écrit cette réponse, j'ai dit :
Eh bien, je l'ai essayé, et les résultats ont été qu'il fonctionnait beaucoup mieux! Voici la requête que j'ai utilisée :
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
Notez que j'ai sélectionné les valeurs en variables pour réduire le temps et la mémoire nécessaires pour tout tester. Le serveur fait toujours le même travail. J'ai modifié la version de Peter pour qu'elle soit similaire et j'ai supprimé les extras inutiles afin qu'ils soient tous les deux aussi légers que possible. La version du serveur utilisée pour ces tests est Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) s'exécutant sur une machine virtuelle.
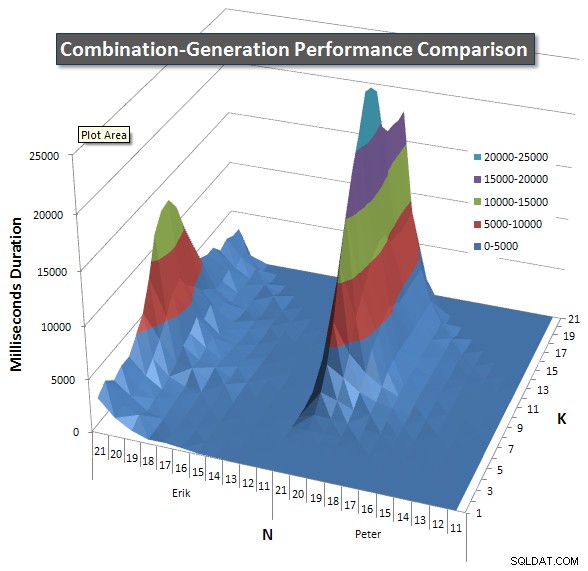
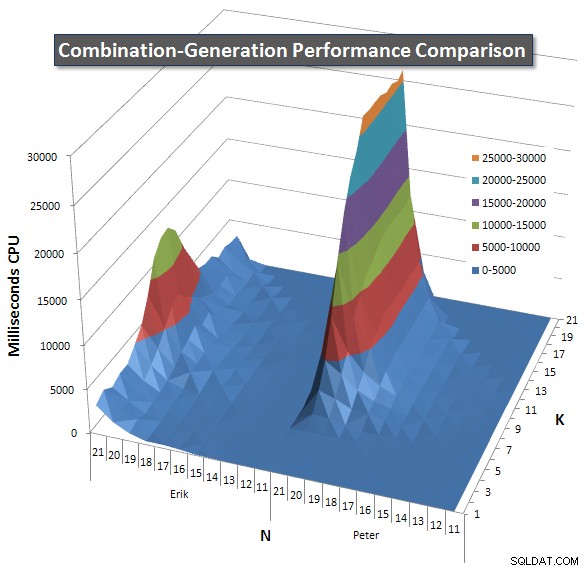
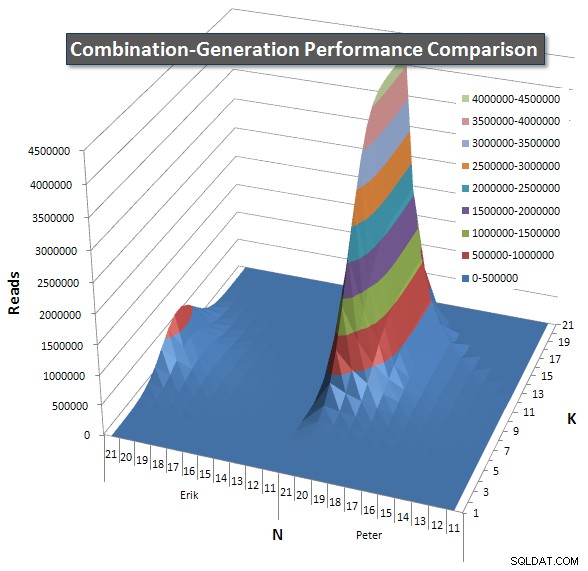
Vous trouverez ci-dessous des graphiques montrant les courbes de performances pour les valeurs de N et K jusqu'à 21. Les données de base pour eux se trouvent dans une autre réponse sur cette page . Les valeurs sont le résultat de 5 exécutions de chaque requête à chaque valeur K et N, suivies de la suppression des meilleures et des pires valeurs pour chaque métrique et de la moyenne des 3 restantes.
Fondamentalement, ma version a une "épaule" (dans le coin le plus à gauche du graphique) à des valeurs élevées de N et des valeurs basses de K qui la rendent moins performante que la version SQL dynamique. Cependant, cela reste assez faible et constant, et le pic central autour de N =21 et K =11 est beaucoup plus faible pour la durée, le processeur et les lectures que la version SQL dynamique.
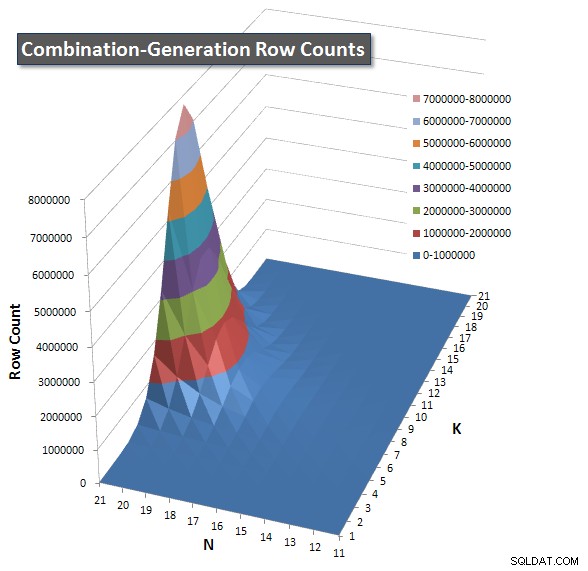
J'ai inclus un tableau du nombre de lignes que chaque élément est censé renvoyer afin que vous puissiez voir comment la requête fonctionne par rapport à l'ampleur du travail qu'elle doit faire.
Veuillez consulter ma réponse supplémentaire sur cette page pour les résultats de performance complets. J'ai atteint la limite de caractères de publication et je n'ai pas pu l'inclure ici. (Avez-vous des idées où le mettre d'autre ?) Pour mettre les choses en perspective par rapport aux résultats de performance de ma première version, voici le même format qu'avant :
Érik
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
Pierre
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
Conclusion
- Les tableaux de nombres à la volée sont meilleurs qu'un vrai tableau contenant des lignes, car la lecture d'un grand nombre de lignes nécessite beaucoup d'E/S. Il vaut mieux utiliser un peu de CPU.
- Mes tests initiaux n'étaient pas assez larges pour vraiment montrer les caractéristiques de performance des deux versions.
- La version de Peter pourrait être améliorée en faisant en sorte que chaque JOIN soit non seulement supérieur à l'élément précédent, mais aussi en restreignant la valeur maximale en fonction du nombre d'éléments supplémentaires à intégrer dans l'ensemble. Par exemple, à 21 éléments pris 21 à la fois, il n'y a qu'une seule réponse de 21 lignes (tous les 21 éléments, une fois), mais les ensembles de lignes intermédiaires dans la version SQL dynamique, au début du plan d'exécution, contiennent des combinaisons telles que " AU" à l'étape 2 même si cela sera ignoré à la prochaine jointure car il n'y a pas de valeur supérieure à "U" disponible. De même, un ensemble de lignes intermédiaire à l'étape 5 contiendra "ARSTU" mais le seul combo valide à ce stade est "ABCDE". Cette version améliorée n'aurait pas de pic inférieur au centre, donc ne l'améliorerait peut-être pas suffisamment pour devenir le grand gagnant, mais elle deviendrait au moins symétrique afin que les graphiques ne restent pas maximisés au-delà du milieu de la région mais retombent. à près de 0 comme le fait ma version (voir le coin supérieur des pics pour chaque requête).
Analyse de durée
- Il n'y a pas de différence vraiment significative entre les versions en durée (>100ms) jusqu'à 14 éléments pris 12 à la fois. Jusqu'à présent, ma version gagne 30 fois et la version SQL dynamique gagne 43 fois.
- À partir de 14•12, ma version était 65 fois plus rapide (59 > 100 ms), la version SQL dynamique 64 fois (60 >100 ms). Cependant, chaque fois que ma version était plus rapide, elle a économisé une durée moyenne totale de 256,5 secondes, et lorsque la version SQL dynamique était plus rapide, elle a économisé 80,2 secondes.
- La durée moyenne totale de tous les essais était de 270,3 secondes pour Erik et de 446,2 secondes pour Peter.
- Si une table de recherche était créée pour déterminer la version à utiliser (en choisissant la plus rapide pour les entrées), tous les résultats pourraient être obtenus en 188,7 secondes. Utiliser le plus lent à chaque fois prendrait 527,7 secondes.
Analyse des lectures
L'analyse de la durée a montré que ma requête gagnait par un montant significatif mais pas trop important. Lorsque la métrique passe aux lectures, une image très différente émerge :ma requête utilise en moyenne 1/10e des lectures.
- Il n'y a pas de différence vraiment significative entre les versions en lectures (>1000) jusqu'à 9 éléments pris 9 à la fois. Jusqu'à présent, ma version gagne 30 fois et la version SQL dynamique gagne 17 fois.
- À partir de 9•9, ma version utilisait moins de lectures 118 fois (113 > 1 000), la version SQL dynamique 69 fois (31 > 1 000). Cependant, chaque fois que ma version utilisait moins de lectures, elle économisait en moyenne 75,9 millions de lectures, et lorsque la version SQL dynamique était plus rapide, elle économisait 380 000 lectures.
- Le nombre total de lectures moyennes pour tous les essais était de 8,4 millions pour Erik et de 84 millions pour Peter.
- Si une table de recherche était créée pour déterminer la version à utiliser (en choisissant la meilleure pour les entrées), tous les résultats pourraient être exécutés en 8 millions de lectures. Utiliser le pire à chaque fois nécessiterait 84,3 millions de lectures.
Je serais très intéressé de voir les résultats d'une version SQL dynamique mise à jour qui place la limite supérieure supplémentaire sur les éléments choisis à chaque étape comme je l'ai décrit ci-dessus.
Avenant
La version suivante de ma requête permet d'obtenir une amélioration d'environ 2,25 % par rapport aux résultats de performances répertoriés ci-dessus. J'ai utilisé la méthode de comptage de bits HAKMEM du MIT et ajouté un Convert(int) sur le résultat de row_number() puisqu'il renvoie un bigint. Bien sûr, j'aurais aimé que ce soit la version que j'ai utilisée pour tous les tests de performances, les graphiques et les données ci-dessus, mais il est peu probable que je la refaite un jour car cela demandait beaucoup de travail.
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
Et je n'ai pas pu résister à montrer une autre version qui fait une recherche pour obtenir le nombre de bits. Il peut même être plus rapide que les autres versions :
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))